Data Structures
Data Structures Overview
Type Aliases
| name | type |
|---|---|
Amount | uint64 |
Graffiti | byte[MAX_GRAFFITI_BYTES] |
HashDigest | byte[32] |
Height | int64 |
Nonce | uint64 |
Round | int32 |
StateSubtreeID | byte |
Timestamp | google.protobuf.Timestamp |
VotingPower | uint64 |
Blockchain Data Structures
Block
Blocks are the top-level data structure of the Celestia blockchain.
| name | type | description |
|---|---|---|
header | Header | Block header. Contains primarily identification info and commitments. |
availableDataHeader | AvailableDataHeader | Header of available data. Contains commitments to erasure-coded data. |
availableData | AvailableData | Data that is erasure-coded for availability. |
lastCommit | Commit | Previous block's Tendermint commit. |
Header
Block header, which is fully downloaded by both full clients and light clients.
| name | type | description |
|---|---|---|
version | ConsensusVersion | The consensus version struct. |
chainID | string | The CHAIN_ID. |
height | Height | Block height. The genesis block is at height 1. |
timestamp | Timestamp | Timestamp of this block. |
lastHeaderHash | HashDigest | Previous block's header hash. |
lastCommitHash | HashDigest | Previous block's Tendermint commit hash. |
consensusHash | HashDigest | Hash of consensus parameters for this block. |
AppHash | HashDigest | The state root after the previous block's transactions are applied. |
availableDataOriginalSharesUsed | uint64 | The number of shares used in the original data square that are not tail padding. |
availableDataRoot | HashDigest | Root of commitments to erasure-coded data. |
proposerAddress | Address | Address of this block's proposer. |
The size of the original data square, availableDataOriginalSquareSize, isn't explicitly declared in the block header. Instead, it is implicitly computed as the smallest power of 2 whose square is at least availableDataOriginalSharesUsed (in other words, the smallest power of 4 that is at least availableDataOriginalSharesUsed).
The header hash is the hash of the serialized header.
AvailableDataHeader
| name | type | description |
|---|---|---|
rowRoots | HashDigest[] | Commitments to all erasure-coded data. |
colRoots | HashDigest[] | Commitments to all erasure-coded data. |
The number of row/column roots of the original data shares in square layout for this block. The availableDataRoot of the header is computed using the compact row and column roots as described in the 2D Reed-Solomon encoding scheme.
The number of row and column roots is each availableDataOriginalSquareSize * 2, and must be a power of 2. Note that the minimum availableDataOriginalSquareSize is 1 (not 0), therefore the number of row and column roots are each at least 2.
Implementations can prune rows containing only tail padding as they are implicitly available.
AvailableData
Data that is erasure-coded for data availability checks.
| name | type | description |
|---|---|---|
transactions | Transaction | Transactions are ordinary Cosmos SDK transactions. For example: they may modify the validator set and token balances. |
payForBlobData | PayForBlobData | PayForBlob data. Transactions that pay for blobs to be included. |
blobData | BlobData | Blob data is arbitrary user submitted data that will be published to the Celestia blockchain. |
Commit
| name | type | description |
|---|---|---|
height | Height | Block height. |
round | Round | Round. Incremented on view change. |
headerHash | HashDigest | Header hash of the previous block. |
signatures | CommitSig[] | List of signatures. |
Timestamp
Timestamp is a type alias.
Celestia uses google.protobuf.Timestamp to represent time.
HashDigest
HashDigest is a type alias.
Output of the hashing function. Exactly 256 bits (32 bytes) long.
TransactionFee
| name | type | description |
|---|---|---|
tipRate | uint64 | The tip rate for this transaction. |
Abstraction over transaction fees.
Address
Celestia supports secp256k1 keys where addresses are 20 bytes in length.
| name | type | description |
|---|---|---|
AccAddress | [20]byte | AccAddress a wrapper around bytes meant to represent an account address |
CommitSig
enum CommitFlag : uint8_t {
CommitFlagAbsent = 1,
CommitFlagCommit = 2,
CommitFlagNil = 3,
};
| name | type | description |
|---|---|---|
commitFlag | CommitFlag | |
validatorAddress | Address | |
timestamp | Timestamp | |
signature | Signature |
Signature
| name | type | description |
|---|---|---|
r | byte[32] | r value of the signature. |
s | byte[32] | s value of signature. |
ConsensusVersion
| name | type | description |
|---|---|---|
block | uint64 | The VERSION_BLOCK. |
app | uint64 | The app version. |
Serialization
Objects that are committed to or signed over require a canonical serialization. This is done using a deterministic (and thus, bijective) variant of protobuf defined in ADR-027.
Note: there are two requirements for a serialization scheme, should this need to be changed:
- Must be bijective.
- Serialization must include the length of dynamic structures (e.g. arrays with variable length).
Hashing
All protocol-level hashing is done using SHA-2-256 as defined in FIPS 180-4. SHA-2-256 outputs a digest that is 256 bits (i.e. 32 bytes) long.
Libraries implementing SHA-2-256 are available in Go (https://pkg.go.dev/crypto/sha256) and Rust (https://docs.rs/sha2/latest/sha2/).
Unless otherwise indicated explicitly, objects are first serialized before being hashed.
Merkle Trees
Merkle trees are used to authenticate various pieces of data across the Celestia stack, including transactions, blobs, the validator set, etc. This section provides an overview of the different tree types used, and specifies how to construct them.
Binary Merkle Tree
Binary Merkle trees are constructed in the same fashion as described in Certificate Transparency (RFC-6962), except for using a different hashing function. Leaves are hashed once to get leaf node values and internal node values are the hash of the concatenation of their children (either leaf nodes or other internal nodes).
Nodes contain a single field:
| name | type | description |
|---|---|---|
v | HashDigest | Node value. |
The base case (an empty tree) is defined as the hash of the empty string:
node.v = 0xe3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855
For leaf node node of leaf data d:
node.v = h(0x00, serialize(d))
For internal node node with children l and r:
node.v = h(0x01, l.v, r.v)
Note that rather than duplicating the last node if there are an odd number of nodes (the Bitcoin design), trees are allowed to be imbalanced. In other words, the height of each leaf may be different. For an example, see Section 2.1.3 of Certificate Transparency (RFC-6962).
Leaves and internal nodes are hashed differently: the one-byte 0x00 is prepended for leaf nodes while 0x01 is prepended for internal nodes. This avoids a second-preimage attack where internal nodes are presented as leaves trees with leaves at different heights.
BinaryMerkleTreeInclusionProof
| name | type | description |
|---|---|---|
siblings | HashDigest[] | Sibling hash values, ordered starting from the leaf's neighbor. |
A proof for a leaf in a binary Merkle tree, as per Section 2.1.1 of Certificate Transparency (RFC-6962).
Namespace Merkle Tree
Shares in Celestia are associated with a provided namespace. The Namespace Merkle Tree (NMT) is a variation of the Merkle Interval Tree, which is itself an extension of the Merkle Sum Tree. It allows for compact proofs around the inclusion or exclusion of shares with particular namespace IDs.
Nodes contain three fields:
| name | type | description |
|---|---|---|
n_min | Namespace | Min namespace in subtree rooted at this node. |
n_max | Namespace | Max namespace in subtree rooted at this node. |
v | HashDigest | Node value. |
The base case (an empty tree) is defined as:
node.n_min = 0x0000000000000000
node.n_max = 0x0000000000000000
node.v = 0xe3b0c44298fc1c149afbf4c8996fb92427ae41e4649b934ca495991b7852b855
For leaf node node of share data d:
node.n_min = d.namespace
node.n_max = d.namespace
node.v = h(0x00, d.namespace, d.rawData)
The namespace blob field here is the namespace of the leaf, which is a NAMESPACE_SIZE-long byte array.
Leaves in an NMT must be lexicographically sorted by namespace in ascending order.
For internal node node with children l and r:
node.n_min = min(l.n_min, r.n_min)
if l.n_min == PARITY_SHARE_NAMESPACE
node.n_max = PARITY_SHARE_NAMESPACE
else if r.n_min == PARITY_SHARE_NAMESPACE
node.n_max = l.n_max
else
node.n_max = max(l.n_max, r.n_max)
node.v = h(0x01, l.n_min, l.n_max, l.v, r.n_min, r.n_max, r.v)
Note that the above snippet leverages the property that leaves are sorted by namespace: if l.n_min is PARITY_SHARE_NAMESPACE, so must {l,r}.n_max. By construction, either both the min and max namespace of a node will be PARITY_SHARE_NAMESPACE, or neither will: if r.n_min is PARITY_SHARE_NAMESPACE, so must r.n_max.
For some intuition: the min and max namespace for subtree roots with at least one non-parity leaf (which includes the root of an NMT, as the right half of an NMT as used in Celestia will be parity shares) ignore the namespace ID for the parity leaves. Subtree roots with only parity leaves have their min and max namespace ID set to PARITY_SHARE_NAMESPACE. This allows for shorter proofs into the tree than if the namespace ID of parity shares was not ignored (which would cause the max namespace ID of the root to always be PARITY_SHARE_NAMESPACE).
A compact commitment can be computed by taking the hash of the serialized root node.
NamespaceMerkleTreeInclusionProof
| name | type | description |
|---|---|---|
siblingValues | HashDigest[] | Sibling hash values, ordered starting from the leaf's neighbor. |
siblingMins | Namespace[] | Sibling min namespace IDs. |
siblingMaxes | Namespace[] | Sibling max namespace IDs. |
When verifying an NMT proof, the root hash is checked by reconstructing the root node root_node with the computed root_node.v (computed as with a plain Merkle proof) and the provided rootNamespaceMin and rootNamespaceMax as the root_node.n_min and root_node.n_max, respectively.
Erasure Coding
In order to enable trust-minimized light clients (i.e. light clients that do not rely on an honest majority of validating state assumption), it is critical that light clients can determine whether the data in each block is available or not, without downloading the whole block itself. The technique used here was formally described in the paper Fraud and Data Availability Proofs: Maximising Light Client Security and Scaling Blockchains with Dishonest Majorities.
The remainder of the subsections below specify the 2D Reed-Solomon erasure coding scheme used, along with the format of shares and how available data is arranged into shares.
Reed-Solomon Erasure Coding
Note that while data is laid out in a two-dimensional square, rows and columns are erasure coded using a standard one-dimensional encoding.
Reed-Solomon erasure coding is used as the underlying coding scheme. The parameters are:
- 16-bit Galois field
availableDataOriginalSquareSizeoriginal pieces (maximum ofAVAILABLE_DATA_ORIGINAL_SQUARE_MAX)availableDataOriginalSquareSizeparity pieces (maximum ofAVAILABLE_DATA_ORIGINAL_SQUARE_MAX) (i.eavailableDataOriginalSquareSize * 2total pieces), for an erasure efficiency of 50%. In other words, any 50% of the pieces from theavailableDataOriginalSquareSize * 2total pieces are enough to recover the original data.SHARE_SIZEbytes per piece
Note that availableDataOriginalSquareSize may vary each block, and is decided by the block proposer of that block. Leopard-RS is a C library that implements the above scheme with quasilinear runtime.
2D Reed-Solomon Encoding Scheme
The 2-dimensional data layout is described in this section. The roots of NMTs for each row and column across four quadrants of data in a 2k * 2k matrix of shares, Q0 to Q3 (shown below), must be computed. In other words, 2k row roots and 2k column roots must be computed. The row and column roots are stored in the availableDataCommitments of the AvailableDataHeader.
The data of Q0 is the original data, and the remaining quadrants are parity data. Setting k = availableDataOriginalSquareSize, the original data first must be split into shares and arranged into a k * k matrix. Then the parity data can be computed.
Where A -> B indicates that B is computed using erasure coding from A:
Q0 -> Q1for each row inQ0andQ1Q0 -> Q2for each column inQ0andQ2Q2 -> Q3for each row inQ2andQ3
Note that the parity data in Q3 will be identical if it is vertically extended from Q1 or horizontally extended from Q2.
As an example, the parity data in the second column of Q2 (in striped purple) is computed by extending the original data in the second column of Q0 (in solid blue).
Now that all four quadrants of the 2k * 2k matrix are filled, the row and column roots can be computed. To do so, each row/column is used as the leaves of a NMT, for which the compact root is computed (i.e. an extra hash operation over the NMT root is used to produce a single HashDigest). In this example, the fourth row root value is computed as the NMT root of the fourth row of Q0 and the fourth row of Q1 as leaves.
Finally, the availableDataRoot of the block Header is computed as the Merkle root of the binary Merkle tree with the row and column roots as leaves, in that order.
Arranging Available Data Into Shares
The previous sections described how some original data, arranged into a k * k matrix, can be extended into a 2k * 2k matrix and committed to with NMT roots. This section specifies how available data (which includes transactions, PayForBlob transactions, and blobs) is arranged into the matrix in the first place.
Note that each share only has a single namespace, and that the list of concatenated shares is lexicographically ordered by namespace.
Then,
- For each of
transactionData,intermediateStateRootData, PayForBlob transactions, serialize:- For each request in the list:
- Serialize the request (individually).
- Compute the length of each serialized request, serialize the length, and prepend the serialized request with its serialized length.
- Split up the length/request pairs into
SHARE_SIZE-NAMESPACE_ID_SIZE-SHARE_RESERVED_BYTES-byte chunks. - Create a share out of each chunk. This data has a reserved namespace ID, so the first
NAMESPACE_SIZE+SHARE_RESERVED_BYTESbytes for these shares must be set specially.
- For each request in the list:
- Concatenate the lists of shares in the order: transactions, intermediate state roots, PayForBlob transactions.
These shares are arranged in the first quadrant (Q0) of the availableDataOriginalSquareSize*2 * availableDataOriginalSquareSize*2 available data matrix in row-major order. In the example below, each reserved data element takes up exactly one share.
Each blob in the list blobData:
- Serialize the blob (individually).
- Compute the length of each serialized blob, serialize the length, and prepend the serialized blob with its serialized length.
- Split up the length/blob pairs into
SHARE_SIZE-NAMESPACE_SIZE-byte chunks. - Create a share out of each chunk. The first
NAMESPACE_SIZEbytes for these shares is set to the namespace.
For each blob, it is placed in the available data matrix, with row-major order, as follows:
- Place the first share of the blob at the next unused location in the matrix, then place the remaining shares in the following locations.
Transactions must commit to a Merkle root of a list of hashes that are each guaranteed (assuming the block is valid) to be subtree roots in one or more of the row NMTs. For additional info, see the rationale document for this section.
However, with only the rule above, interaction between the block producer and transaction sender may be required to compute a commitment to the blob the transaction sender can sign over. To remove interaction, blobs can optionally be laid out using a non-interactive default:
- Place the first share of the blob at the next unused location in the matrix whose column is aligned with the largest power of 2 that is not larger than the blob length or
availableDataOriginalSquareSize, then place the remaining shares in the following locations unless there are insufficient unused locations in the row. - If there are insufficient unused locations in the row, place the first share of the blob at the first column of the next row. Then place the remaining shares in the following locations. By construction, any blob whose length is greater than
availableDataOriginalSquareSizewill be placed in this way.
In the example below, two blobs (of lengths 2 and 1, respectively) are placed using the aforementioned default non-interactive rules.
The blob share commitment rules may introduce empty shares that do not belong to any blob (in the example above, the top-right share is empty). These are zeroes with namespace ID equal to the either TAIL_TRANSACTION_PADDING_NAMESPACE_ID if between a request with a reserved namespace ID and a blob, or the namespace ID of the previous blob if succeeded by a blob. See the data square layout for more info.
Available Data
Transaction
Celestia transactions are Cosmos SDK transactions.
PayForBlobData
IndexWrapper
IndexWrapper are wrappers around PayForBlob transactions. They include additional metadata by the block proposer that is committed to in the available data matrix.
| name | type | description |
|---|---|---|
tx | bytes | Actual transaction. |
share_indexes | []uint32 | Share indexes (in row-major order) of the first share for each blob this transaction pays for. Needed for light verification of proper blob inclusion. |
type_id | string | Type ID of the IndexWrapper transaction type. This is used for encoding and decoding IndexWrapper transactions. It is always set to "INDX". |
BlobData
| name | type | description |
|---|---|---|
blobs | Blob[] | List of blobs. |
Blob
| name | type | description |
|---|---|---|
namespaceID | NamespaceID | Namespace ID of this blob. |
rawData | byte[] | Raw blob bytes. |
State
The state of the Celestia chain is intentionally restricted to containing only account balances and the validator set metadata. Similar to other Cosmos SDK based chains, the state of the Celestia chain is maintained in a multistore. The root of the application state is committed to in the block header via the AppHash.
Consensus Parameters
Various consensus parameters are committed to in the block header, such as limits and constants.
| name | type | description |
|---|---|---|
version | ConsensusVersion | The consensus version struct. |
chainID | string | The CHAIN_ID. |
shareSize | uint64 | The SHARE_SIZE. |
shareReservedBytes | uint64 | The SHARE_RESERVED_BYTES. |
availableDataOriginalSquareMax | uint64 | The AVAILABLE_DATA_ORIGINAL_SQUARE_MAX. |
In order to compute the consensusHash field in the block header, the above list of parameters is hashed.
Namespace
Abstract
One of Celestia's core data structures is the namespace.
When a user submits a transaction encapsulating a MsgPayForBlobs message to Celestia, they MUST associate each blob with exactly one namespace.
After their transaction has been included in a block, the namespace enables users to take an interest in a subset of the blobs published to Celestia by allowing the user to query for blobs by namespace.
In order to enable efficient retrieval of blobs by namespace, Celestia makes use of a Namespaced Merkle Tree. See section 5.2 of the LazyLedger whitepaper for more details.
Overview
A namespace is composed of two fields: version and id. A namespace is encoded as a byte slice with the version and id concatenated.
Version
The namespace version is an 8-bit unsigned integer that indicates the version of the namespace. The version is used to determine the format of the namespace and is encoded as a single byte. A new namespace version MUST be introduced if the namespace format changes in a backwards incompatible way.
Below we explain supported user-specifiable namespace versions, however, we note that Celestia MAY utilize other namespace versions for internal use. For more details, see the Reserved Namespaces section.
Version 0
The only supported user-specifiable namespace version is 0.
A namespace with version 0 MUST contain an id with a prefix of 18 leading 0 bytes.
The remaining 10 bytes of the id are user-specified.
Below, we provide examples of valid and invalid encoded user-supplied namespaces with version 0.
// Valid encoded namespaces
0x0000000000000000000000000000000000000001010101010101010101 // valid blob namespace
0x0000000000000000000000000000000000000011111111111111111111 // valid blob namespace
// Invalid encoded namespaces
0x0000000000000000000000000111111111111111111111111111111111 // invalid because it does not have 18 leading 0 bytes
0x1000000000000000000000000000000000000000000000000000000000 // invalid because it does not have version 0
0x1111111111111111111111111111111111111111111111111111111111 // invalid because it does not have version 0
Any change in the number of leading 0 bytes in the id of a namespace with version 0 is considered a backwards incompatible change and MUST be introduced as a new namespace version.
ID
The namespace ID is a 28 byte identifier that uniquely identifies a namespace. The ID is encoded as a byte slice of length 28.
Reserved Namespaces
Celestia reserves some namespaces for protocol use. These namespaces are called "reserved namespaces". Reserved namespaces are used to arrange the contents of the data square. Applications MUST NOT use reserved namespaces for their blob data. Reserved namespaces fall into two categories: Primary and Secondary.
- Primary: Namespaces with values less than or equal to
0x00000000000000000000000000000000000000000000000000000000FF. Primary namespaces always have a version of0. - Secondary: Namespaces with values greater than or equal to
0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00. Secondary namespaces always have a version of255(0xFF) so that they are placed after all user specifiable namespaces in a sorted data square. ThePARITY_SHARE_NAMESPACEuses version255(0xFF) to enable more efficient proof generation within the context of nmt, where it is used in conjunction with theIgnoreMaxNamespacefeature. TheTAIL_PADDING_NAMESPACEuses the version255to ensure that padding shares are always placed at the end of the Celestia data square even if a new user-specifiable version is introduced.
Below is a list of the current reserved namespaces. For additional information on the significance and application of the reserved namespaces, please refer to the Data Square Layout specifications.
| name | type | category | value | description |
|---|---|---|---|---|
TRANSACTION_NAMESPACE | Namespace | Primary | 0x0000000000000000000000000000000000000000000000000000000001 | Namespace for ordinary Cosmos SDK transactions. |
INTERMEDIATE_STATE_ROOT_NAMESPACE | Namespace | Primary | 0x0000000000000000000000000000000000000000000000000000000002 | Namespace for intermediate state roots (not currently utilized). |
PAY_FOR_BLOB_NAMESPACE | Namespace | Primary | 0x0000000000000000000000000000000000000000000000000000000004 | Namespace for transactions that contain a PayForBlob. |
PRIMARY_RESERVED_PADDING_NAMESPACE | Namespace | Primary | 0x00000000000000000000000000000000000000000000000000000000FF | Namespace for padding after all primary reserved namespaces. |
MAX_PRIMARY_RESERVED_NAMESPACE | Namespace | Primary | 0x00000000000000000000000000000000000000000000000000000000FF | Namespace for the highest primary reserved namespace. |
MIN_SECONDARY_RESERVED_NAMESPACE | Namespace | Secondary | 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00 | Namespace for the lowest secondary reserved namespace. |
TAIL_PADDING_NAMESPACE | Namespace | Secondary | 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFE | Namespace for padding after all blobs to fill up the original data square. |
PARITY_SHARE_NAMESPACE | Namespace | Secondary | 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF | Namespace for parity shares. |
Assumptions and Considerations
Applications MUST refrain from using the reserved namespaces for their blob data.
Celestia does not ensure the prevention of non-reserved namespace collisions. Consequently, two distinct applications might use the same namespace. It is the responsibility of these applications to be cautious and manage the implications and consequences arising from such namespace collisions. Among the potential consequences is the Woods Attack, as elaborated in this forum post: Woods Attack on Celestia.
Implementation
See the namespace implementation in go-square. For the most recent version, which may not reflect the current specifications, refer to the latest namespace code.
Go Definition
type Namespace struct {
Version uint8
ID []byte
}
References
Shares
Abstract
All available data in a Celestia block is split into fixed-size data chunks known as "shares". Shares are the atomic unit of the Celestia data square. The shares in a Celestia block are eventually erasure-coded and committed to in Namespace Merkle trees (also see NMT spec).
Terms
- Blob: User specified data (e.g. a roll-up block) that is associated with exactly one namespace. Blob data are opaque bytes of data that are included in the block but do not impact Celestia's state.
- Share: A fixed-size data chunk that is associated with exactly one namespace.
- Share sequence: A share sequence is a contiguous set of shares that contain semantically relevant data. A share sequence MUST contain one or more shares. When a blob is split into shares, it is written to one share sequence. As a result, all shares in a share sequence are typically parsed together because the original blob data may have been split across share boundaries. All transactions in the
TRANSACTION_NAMESPACEare contained in one share sequence. All transactions in thePAY_FOR_BLOB_NAMESPACEare contained in one share sequence.
Overview
User submitted transactions are split into shares (see share splitting) and arranged in a k * k matrix (see arranging available data into shares) prior to the erasure coding step. Shares in the k * k matrix are ordered by namespace and have a common share format.
Padding shares are added to the k * k matrix to ensure:
- Blob sequences start on an index that conforms to blob share commitment rules (see namespace padding share and reserved padding share)
- The number of shares in the matrix is a perfect square (see tail padding share)
Share Format
Share Version
The share version is a 7-bit big-endian unsigned integer that is used to indicate the version of the share format. A new share version MUST be introduced if the share format changes in a way that is not backwards compatible. There are two share versions share version 0 and share version 1.
Share Version 0
Every share has a fixed size SHARE_SIZE. The share format below is consistent for all shares:
- The first
NAMESPACE_VERSION_SIZEbytes of a share's raw data is the namespace version of that share (denoted by "namespace version" in the figure below). - The next
NAMESPACE_ID_SIZEbytes of a share's raw data is the namespace ID of that share (denoted by "namespace id" in the figure below). - The next
SHARE_INFO_BYTESbytes are for share information (denoted by "info byte" in the figure below) with the following structure:- The first 7 bits represent the share version in big endian form (initially, this will be
0000000for version0); - The last bit is a sequence start indicator. The indicator is
1if this share is the first share in a sequence or0if this share is a continuation share in a sequence.
- The first 7 bits represent the share version in big endian form (initially, this will be
- If this share is the first share in a sequence, it will include the length of the sequence in bytes. The next
SEQUENCE_BYTESrepresent a big-endian uint32 value (denoted by "sequence length" in the figure below). This length is placed immediately after theSHARE_INFO_BYTESfield. It's important to note that shares that are not the first share in a sequence do not contain this field. - The remaining
SHARE_SIZE-NAMESPACE_SIZE-SHARE_INFO_BYTES-SEQUENCE_BYTESbytes (if first share) orSHARE_SIZE-NAMESPACE_SIZE-SHARE_INFO_BYTESbytes (if continuation share) are raw data (denoted by "blob1" in the figure below). Typically raw data is the blob payload that user's submit in a BlobTx. However, raw data can also be transaction data (see transaction shares below). - If there is insufficient raw data to fill the share, the remaining bytes are filled with
0.
First share in a sequence:
Continuation share in a sequence:
Since raw data that exceeds SHARE_SIZE-NAMESPACE_SIZE-SHARE_INFO_BYTES - SEQUENCE_BYTES bytes will span more than one share, developers MAY choose to encode additional metadata in their raw blob data prior to inclusion in a Celestia block. For example, Celestia transaction shares encode additional metadata in the form of "reserved bytes".
Share Version 1
Share version 1 is similar to share version 0 with the addition of a signer field. The signer is located after the sequence length in the first share. The signer is SIGNER_SIZE bytes.
First share in a sequence with signer:
Continuation share in a sequence:
Transaction Shares
Transaction shares use share version 0. In order for clients to parse shares in the middle of a sequence without downloading antecedent shares, Celestia encodes additional metadata in the shares associated with reserved namespaces. At the time of writing this only applies to the TRANSACTION_NAMESPACE and PAY_FOR_BLOB_NAMESPACE. This share structure is often referred to as "compact shares" to differentiate from the share structure defined above for all shares. It conforms to the common share format with one additional field, the "reserved bytes" field, which is described below:
- Every transaction share includes
SHARE_RESERVED_BYTESbytes that contain the index of the starting byte of the length of the canonically serialized first transaction that starts in the share, or0if there is none, as a binary big endianuint32. Denoted by "reserved bytes" in the figure below. TheSHARE_RESERVED_BYTESare placed immediately after theSEQUENCE_BYTESif this is the first share in a sequence or immediately after theSHARE_INFO_BYTESif this is a continuation share in a sequence. - The remaining
SHARE_SIZE-NAMESPACE_SIZE-SHARE_INFO_BYTES-SEQUENCE_BYTES-SHARE_RESERVED_BYTESbytes (if first share) orSHARE_SIZE-NAMESPACE_SIZE-SHARE_INFO_BYTES-SHARE_RESERVED_BYTESbytes (if continuation share) are transaction or PayForBlob transaction data (denoted by "tx1" and "tx2" in the figure below). Each transaction or PayForBlob transaction is prefixed with a varint of the length of that unit (denoted by "len(tx1)" and "len(tx2)" in the figure below). - If there is insufficient transaction or PayForBlob transaction data to fill the share, the remaining bytes are filled with
0.
First share in a sequence:
where reserved bytes would be 38 as a binary big endian uint32 ([0b00000000, 0b00000000, 0b00000000, 0b00100110]).
Continuation share in a sequence:
where reserved bytes would be 80 as a binary big endian uint32 ([0b00000000, 0b00000000, 0b00000000, 0b01010000]).
Padding
Padding shares use share version 0 and conform to the share format described above. There are multiple variants of padding shares that differ based on their namespace.
- The first
NAMESPACE_VERSION_SIZEbytes of a share's raw data is the namespace version of that share (initially, this will be0). - The next
NAMESPACE_ID_SIZEbytes of a share's raw data is the namespace ID of that share. This varies based on the type of padding share. - The next
SHARE_INFO_BYTESbytes are for share information.- The first 7 bits represent the share version in big endian form (initially, this will be
0000000for version0); - The last bit is a sequence start indicator. The indicator is always
1.
- The first 7 bits represent the share version in big endian form (initially, this will be
- The next
SEQUENCE_BYTEScontain a big endianuint32of value0. - The remaining
SHARE_SIZE-NAMESPACE_SIZE-SHARE_INFO_BYTES-SEQUENCE_BYTESbytes are filled with0.
Namespace Padding Share
A namespace padding share uses the namespace of the blob that precedes it in the data square so that the data square can retain the property that all shares are ordered by namespace. A namespace padding share acts as padding between blobs so that the subsequent blob begins at an index that conforms to the blob share commitment rules. Clients MAY ignore the contents of these shares because they don't contain any significant data.
Primary Reserved Padding Share
Primary reserved padding shares use the PRIMARY_RESERVED_PADDING_NAMESPACE. Primary reserved padding shares are placed after shares in the primary reserved namespace range so that the first blob can start at an index that conforms to blob share commitment rules. Clients MAY ignore the contents of these shares because they don't contain any significant data.
Tail Padding Share
Tail padding shares use the TAIL_PADDING_NAMESPACE. Tail padding shares are placed after the last blob in the data square so that the number of shares in the data square is a perfect square. Clients MAY ignore the contents of these shares because they don't contain any significant data.
Parity Share
Parity shares are the output of the erasure coding step of the data square construction process. They occupy quadrants Q1, Q2, and Q3 of the extended data square and are used to reconstruct the original data square (Q0). Parity shares do not conform to the share format described above. In the square layout, parity shares do not have a significant namespace. When parity shares are used in NMTs, they are prefixed with the PARITY_SHARE_NAMESPACE to preserve the property that all shares are ordered by namespace.
Share Splitting
Share splitting is the process of converting a blob into a share sequence. The process is as follows:
- Create a new share and populate the prefix of the share with the blob's namespace and share version. Set the sequence start indicator to
1. Write the blob length as the sequence length. Write the blob's data into the share until the share is full. - If there is more data to write, create a new share (a.k.a continuation share) and populate the prefix of the share with the blob's namespace and share version. Set the sequence start indicator to
0. Write the remaining blob data into the share until the share is full. - Repeat the previous step until all blob data has been written.
- If the last share is not full, fill the remainder of the share with
0.
Assumptions and Considerations
- Shares are assumed to be byte slices of length 512. Parsing shares of a different length WILL result in an error.
Implementation
See go-square/shares.
References
Consensus Rules
System Parameters
Units
| name | SI | value | description |
|---|---|---|---|
1u | 1u | 10**0 | 1 unit. |
2u | k1u | 10**3 | 1000 units. |
3u | M1u | 10**6 | 1000000 units. |
4u | G1u | 10**9 | 1000000000 units. |
Constants
| name | type | value | unit | description |
|---|---|---|---|---|
AVAILABLE_DATA_ORIGINAL_SQUARE_MAX | uint64 | share | Maximum number of rows/columns of the original data shares in square layout. | |
AVAILABLE_DATA_ORIGINAL_SQUARE_TARGET | uint64 | share | Target number of rows/columns of the original data shares in square layout. | |
BLOCK_TIME | uint64 | second | Block time, in seconds. | |
CHAIN_ID | string | "Celestia" | Chain ID. Each chain assigns itself a (unique) ID. | |
GENESIS_COIN_COUNT | uint64 | 10**8 | 4u | (= 100000000) Number of coins at genesis. |
MAX_GRAFFITI_BYTES | uint64 | 32 | byte | Maximum size of transaction graffiti, in bytes. |
MAX_VALIDATORS | uint16 | 64 | Maximum number of active validators. | |
NAMESPACE_VERSION_SIZE | int | 1 | byte | Size of namespace version in bytes. |
NAMESPACE_ID_SIZE | int | 28 | byte | Size of namespace ID in bytes. |
NAMESPACE_SIZE | int | 29 | byte | Size of namespace in bytes. |
NAMESPACE_ID_MAX_RESERVED | uint64 | 255 | Value of maximum reserved namespace (inclusive). 1 byte worth of IDs. | |
SEQUENCE_BYTES | uint64 | 4 | byte | The number of bytes used to store the sequence length in the first share of a sequence |
SHARE_INFO_BYTES | uint64 | 1 | byte | The number of bytes used for share information |
SHARE_RESERVED_BYTES | uint64 | 4 | byte | The number of bytes used to store the index of the first transaction in a transaction share. Must be able to represent any integer up to and including SHARE_SIZE - 1. |
SHARE_SIZE | uint64 | 512 | byte | Size of transaction and blob shares, in bytes. |
SignerSize | int | 20 | byte | The number of bytes used to store the signer in a share. |
STATE_SUBTREE_RESERVED_BYTES | uint64 | 1 | byte | Number of bytes reserved to identify state subtrees. |
UNBONDING_DURATION | uint32 | block | Duration, in blocks, for unbonding a validator or delegation. | |
v1.Version | uint64 | 1 | First version of the application. Breaking changes (hard forks) must update this parameter. | |
v2.Version | uint64 | 2 | Second version of the application. Breaking changes (hard forks) must update this parameter. | |
VERSION_BLOCK | uint64 | 1 | Version of the Celestia chain. Breaking changes (hard forks) must update this parameter. |
Rewards and Penalties
| name | type | value | unit | description |
|---|---|---|---|---|
SECONDS_PER_YEAR | uint64 | 31536000 | second | Seconds per year. Omit leap seconds. |
TARGET_ANNUAL_ISSUANCE | uint64 | 2 * 10**6 | 4u | (= 2000000) Target number of coins to issue per year. |
Leader Selection
Refer to the CometBFT specifications for proposer selection procedure.
Fork Choice
The Tendermint consensus protocol is fork-free by construction under an honest majority of stake assumption.
If a block has a valid commit, it is part of the canonical chain. If equivocation evidence is detected for more than 1/3 of voting power, the node must halt. See proof of fork accountability.
Block Validity
The validity of a newly-seen block, block, is determined by two components, detailed in subsequent sections:
- Block structure: whether the block header is valid, and data in a block is arranged into a valid and matching data root (i.e. syntax).
- State transition: whether the application of transactions in the block produces a matching and valid state root (i.e. semantics).
Pseudocode in this section is not in any specific language and should be interpreted as being in a neutral and sane language.
Block Structure
Before executing state transitions, the structure of the block must be verified.
The following block fields are acquired from the network and parsed (i.e. deserialized). If they cannot be parsed, the block is ignored but is not explicitly considered invalid by consensus rules. Further implications of ignoring a block are found in the networking spec.
If the above fields are parsed successfully, the available data block.availableData is acquired in erasure-coded form as a list of share rows, then parsed. If it cannot be parsed, the block is ignored but not explicitly invalid, as above.
block.header
The block header block.header (header for short) is the first thing that is downloaded from the new block, and commits to everything inside the block in some way. For previous block prev (if prev is not known, then the block is ignored), and previous block header prev.header, the following checks must be true:
availableDataOriginalSquareSize is computed as described in the header section.
header.height==prev.header.height + 1.header.timestamp>prev.header.timestamp.header.lastHeaderHash== the header hash ofprev.header.lastCommitHash== the hash oflastCommit.header.consensusHash== the value computed using consensus parameters.header.stateCommitment== the root of the state, computed with the application of all state transitions in this block.availableDataOriginalSquareSize<=AVAILABLE_DATA_ORIGINAL_SQUARE_MAX.header.availableDataRoot== the Merkle root of the tree with the row and column roots ofblock.availableDataHeaderas leaves.header.proposerAddress== the leader forheader.height.
block.availableDataHeader
The available data header block.availableDataHeader (availableDataHeader for short) is then processed. This commits to the available data, which is only downloaded after the consensus commit is processed. The following checks must be true:
- Length of
availableDataHeader.rowRoots==availableDataOriginalSquareSize * 2. - Length of
availableDataHeader.colRoots==availableDataOriginalSquareSize * 2. - The length of each element in
availableDataHeader.rowRootsandavailableDataHeader.colRootsmust be32.
block.lastCommit
The last commit block.lastCommit (lastCommit for short) is processed next. This is the Tendermint commit (i.e. polka of votes) for the previous block. For previous block prev and previous block header prev.header, the following checks must be true:
lastCommit.height==prev.header.height.lastCommit.round>=1.lastCommit.headerHash== the header hash ofprev.- Length of
lastCommit.signatures<=MAX_VALIDATORS. - Each of
lastCommit.signaturesmust be a valid CommitSig - The sum of the votes for
previnlastCommitmust be at least 2/3 (rounded up) of the voting power ofprev's next validator set.
block.availableData
The block's available data (analogous to transactions in contemporary blockchain designs) block.availableData (availableData for short) is finally processed. The list of share rows is parsed into the actual data structures using the reverse of the process to encode available data into shares; if parsing fails here, the block is invalid.
Once parsed, the following checks must be true:
- The commitments of the erasure-coded extended
availableDatamust match those inheader.availableDataHeader. Implicitly, this means that both rows and columns must be ordered lexicographically by namespace since they are committed to in a Namespace Merkle Tree. - Length of
availableData.intermediateStateRootData== length ofavailableData.transactionData+ length ofavailableData.payForBlobData+ 2. (Two additional state transitions are the begin and end block implicit transitions.)
State Transitions
Once the basic structure of the block has been validated, state transitions must be applied to compute the new state and state root.
For this section, the variable state represents the state tree, with state.accounts[k], state.inactiveValidatorSet[k], state.activeValidatorSet[k], and state.delegationSet[k] being shorthand for the leaf in the state tree in the accounts, inactive validator set, active validator set, and delegation set subtrees with pre-hashed key k. E.g. state.accounts[a] is shorthand for state[(ACCOUNTS_SUBTREE_ID << 8*(32-STATE_SUBTREE_RESERVED_BYTES)) | ((-1 >> 8*STATE_SUBTREE_RESERVED_BYTES) & hash(a))].
State transitions are applied in the following order:
block.availableData.transactionData
Transactions are applied to the state. Note that transactions mutate the state (essentially, the validator set and minimal balances), while blobs do not.
block.availableData.transactionData is simply a list of WrappedTransactions. For each wrapped transaction in this list, wrappedTransaction, with index i (starting from 0), the following checks must be true:
wrappedTransaction.index==i.
For wrappedTransaction's transaction transaction, the following checks must be true:
transaction.signaturemust be a valid signature overtransaction.signedTransactionData.
Finally, each wrappedTransaction is processed depending on its transaction type. These are specified in the next subsections, where tx is short for transaction.signedTransactionData, and sender is the recovered signing address. We will define a few helper functions:
tipCost(y, z) = y * z
totalCost(x, y, z) = x + tipCost(y, z)
where x above is the amount of coins sent by the transaction authorizer, y above is the tip rate set in the transaction, and z above is the measure of the block space used by the transaction (i.e. size in bytes).
Four additional helper functions are defined to manage the validator queue:
-
findFromQueue(power), which returns the address of the last validator in the validator queue with voting power greater than or equal topower, or0if the queue is empty or no validators in the queue have at leastpowervoting power. -
parentFromQueue(address), which returns the address of the parent in the validator queue of the validator with addressaddress, or0ifaddressis not in the queue or is the head of the queue. -
validatorQueueInsert, defined asfunction validatorQueueInsert(validator) # Insert the new validator into the linked list parent = findFromQueue(validator.votingPower) if parent != 0 if state.accounts[parent].status == AccountStatus.ValidatorBonded validator.next = state.activeValidatorSet[parent].next state.activeValidatorSet[parent].next = sender else validator.next = state.inactiveValidatorSet[parent].next state.inactiveValidatorSet[parent].next = sender else validator.next = state.validatorQueueHead state.validatorQueueHead = sender
-
validatorQueueRemove, defined asfunction validatorQueueRemove(validator, sender) # Remove existing validator from the linked list parent = parentFromQueue(sender) if parent != 0 if state.accounts[parent].status == AccountStatus.ValidatorBonded state.activeValidatorSet[parent].next = validator.next validator.next = 0 else state.inactiveValidatorSet[parent].next = validator.next validator.next = 0 else state.validatorQueueHead = validator.next validator.next = 0
Note that light clients cannot perform a linear search through a linked list, and are instead provided logarithmic proofs (e.g. in the case of parentFromQueue, a proof to the parent is provided, which should have address as its next validator).
In addition, three helper functions to manage the blob paid list:
findFromBlobPaidList(start), which returns the transaction ID of the last transaction in the blob paid list withfinishgreater thanstart, or0if the list is empty or no transactions in the list have at leaststartfinish.parentFromBlobPaidList(txid), which returns the transaction ID of the parent in the blob paid list of the transaction with IDtxid, or0iftxidis not in the list or is the head of the list.blobPaidListInsert, defined as
function blobPaidListInsert(tx, txid)
# Insert the new transaction into the linked list
parent = findFromBlobPaidList(tx.blobStartIndex)
state.blobsPaid[txid].start = tx.blobStartIndex
numShares = ceil(tx.blobSize / SHARE_SIZE)
state.blobsPaid[txid].finish = tx.blobStartIndex + numShares - 1
if parent != 0
state.blobsPaid[txid].next = state.blobsPaid[parent].next
state.blobsPaid[parent].next = txid
else
state.blobsPaid[txid].next = state.blobPaidHead
state.blobPaidHead = txid
We define a helper function to compute F1 entries:
function compute_new_entry(reward, power)
if power == 0
return 0
return reward // power
After applying a transaction, the new state root is computed.
SignedTransactionDataTransfer
bytesPaid = len(tx)
The following checks must be true:
tx.type==TransactionType.Transfer.totalCost(tx.amount, tx.fee.tipRate, bytesPaid)<=state.accounts[sender].balance.tx.nonce==state.accounts[sender].nonce + 1.
Apply the following to the state:
state.accounts[sender].nonce += 1
state.accounts[sender].balance -= totalCost(tx.amount, tx.fee.tipRate, bytesPaid)
state.accounts[tx.to].balance += tx.amount
state.activeValidatorSet.proposerBlockReward += tipCost(bytesPaid)
SignedTransactionDataMsgPayForData
bytesPaid = len(tx) + tx.blobSize
currentStartFinish = state.blobsPaid[findFromBlobPaidList(tx.blobStartIndex)]
parentStartFinish = state.blobsPaid[parentFromBlobPaidList(findFromBlobPaidList(tx.blobStartIndex))]
The following checks must be true:
tx.type==TransactionType.MsgPayForData.totalCost(0, tx.fee.tipRate, bytesPaid)<=state.accounts[sender].balance.tx.nonce==state.accounts[sender].nonce + 1.- The
ceil(tx.blobSize / SHARE_SIZE)shares starting at indextx.blobStartIndexmust:- Have namespace
tx.blobNamespace.
- Have namespace
tx.blobShareCommitment== computed as described in the MsgPayForData section.parentStartFinish.finish<tx.blobStartIndex.currentStartFinish.start==0orcurrentStartFinish.start>tx.blobStartIndex + ceil(tx.blobSize / SHARE_SIZE).
Apply the following to the state:
state.accounts[sender].nonce += 1
state.accounts[sender].balance -= totalCost(tx.amount, tx.fee.tipRate, bytesPaid)
blobPaidListInsert(tx, id(tx))
state.activeValidatorSet.proposerBlockReward += tipCost(tx.fee.tipRate, bytesPaid)
SignedTransactionDataCreateValidator
bytesPaid = len(tx)
The following checks must be true:
tx.type==TransactionType.CreateValidator.totalCost(0, tx.fee.tipRate, bytesPaid)<=state.accounts[sender].balance.tx.nonce==state.accounts[sender].nonce + 1.tx.commissionRate.denominator > 0.tx.commissionRate.numerator <= tx.commissionRate.denominator.state.accounts[sender].status==AccountStatus.None.
Apply the following to the state:
state.accounts[sender].nonce += 1
state.accounts[sender].balance -= totalCost(0, tx.fee.tipRate, bytesPaid)
state.accounts[sender].status = AccountStatus.ValidatorQueued
validator = new Validator
validator.commissionRate = tx.commissionRate
validator.delegatedCount = 0
validator.votingPower = 0
validator.pendingRewards = 0
validator.latestEntry = PeriodEntry(0)
validator.unbondingHeight = 0
validator.isSlashed = false
validatorQueueInsert(validator)
state.inactiveValidatorSet[sender] = validator
state.activeValidatorSet.proposerBlockReward += tipCost(tx.fee.tipRate, bytesPaid)
SignedTransactionDataBeginUnbondingValidator
bytesPaid = len(tx)
The following checks must be true:
tx.type==TransactionType.BeginUnbondingValidator.totalCost(0, tx.fee.tipRate, bytesPaid)<=state.accounts[sender].balance.tx.nonce==state.accounts[sender].nonce + 1.state.accounts[sender].status==AccountStatus.ValidatorQueuedorstate.accounts[sender].status==AccountStatus.ValidatorBonded.
Apply the following to the state:
state.accounts[sender].nonce += 1
state.accounts[sender].balance -= totalCost(0, tx.fee.tipRate, bytesPaid)
state.accounts[sender].status = ValidatorStatus.Unbonding
if state.accounts[sender].status == AccountStatus.ValidatorQueued
validator = state.inactiveValidatorSet[sender]
else if state.accounts[sender].status == AccountStatus.ValidatorBonded
validator = state.activeValidatorSet[sender]
delete state.activeValidatorSet[sender]
validator.unbondingHeight = block.height + 1
validator.latestEntry += compute_new_entry(validator.pendingRewards, validator.votingPower)
validator.pendingRewards = 0
validatorQueueRemove(validator, sender)
state.inactiveValidatorSet[sender] = validator
state.activeValidatorSet.activeVotingPower -= validator.votingPower
state.activeValidatorSet.proposerBlockReward += tipCost(tx.fee.tipRate, bytesPaid)
SignedTransactionDataUnbondValidator
bytesPaid = len(tx)
The following checks must be true:
tx.type==TransactionType.UnbondValidator.totalCost(0, tx.fee.tipRate, bytesPaid)<=state.accounts[sender].balance.tx.nonce==state.accounts[sender].nonce + 1.state.accounts[sender].status==AccountStatus.ValidatorUnbonding.state.inactiveValidatorSet[sender].unbondingHeight + UNBONDING_DURATION<block.height.
Apply the following to the state:
validator = state.inactiveValidatorSet[sender]
state.accounts[sender].nonce += 1
state.accounts[sender].balance -= totalCost(0, tx.fee.tipRate, bytesPaid)
state.accounts[sender].status = AccountStatus.ValidatorUnbonded
state.accounts[sender].balance += validator.commissionRewards
state.inactiveValidatorSet[sender] = validator
if validator.delegatedCount == 0
state.accounts[sender].status = AccountStatus.None
delete state.inactiveValidatorSet[sender]
state.activeValidatorSet.proposerBlockReward += tipCost(tx.fee.tipRate, bytesPaid)
SignedTransactionDataCreateDelegation
bytesPaid = len(tx)
The following checks must be true:
tx.type==TransactionType.CreateDelegation.totalCost(tx.amount, tx.fee.tipRate, bytesPaid)<=state.accounts[sender].balance.state.accounts[tx.to].status==AccountStatus.ValidatorQueuedorstate.accounts[tx.to].status==AccountStatus.ValidatorBonded.tx.nonce==state.accounts[sender].nonce + 1.state.accounts[sender].status==AccountStatus.None.
Apply the following to the state:
state.accounts[sender].nonce += 1
state.accounts[sender].balance -= totalCost(tx.amount, tx.fee.tipRate, bytesPaid)
state.accounts[sender].status = AccountStatus.DelegationBonded
if state.accounts[tx.to].status == AccountStatus.ValidatorQueued
validator = state.inactiveValidatorSet[tx.to]
else if state.accounts[tx.to].status == AccountStatus.ValidatorBonded
validator = state.activeValidatorSet[tx.to]
delegation = new Delegation
delegation.status = DelegationStatus.Bonded
delegation.validator = tx.to
delegation.stakedBalance = tx.amount
delegation.beginEntry = validator.latestEntry
delegation.endEntry = PeriodEntry(0)
delegation.unbondingHeight = 0
validator.latestEntry += compute_new_entry(validator.pendingRewards, validator.votingPower)
validator.pendingRewards = 0
validator.delegatedCount += 1
validator.votingPower += tx.amount
# Update the validator in the linked list by first removing then inserting
validatorQueueRemove(validator, delegation.validator)
validatorQueueInsert(validator)
state.delegationSet[sender] = delegation
if state.accounts[tx.to].status == AccountStatus.ValidatorQueued
state.inactiveValidatorSet[tx.to] = validator
else if state.accounts[tx.to].status == AccountStatus.ValidatorBonded
state.activeValidatorSet[tx.to] = validator
state.activeValidatorSet.activeVotingPower += tx.amount
state.activeValidatorSet.proposerBlockReward += tipCost(tx.fee.tipRate, bytesPaid)
SignedTransactionDataBeginUnbondingDelegation
bytesPaid = len(tx)
The following checks must be true:
tx.type==TransactionType.BeginUnbondingDelegation.totalCost(0, tx.fee.tipRate, bytesPaid)<=state.accounts[sender].balance.tx.nonce==state.accounts[sender].nonce + 1.state.accounts[sender].status==AccountStatus.DelegationBonded.
Apply the following to the state:
state.accounts[sender].nonce += 1
state.accounts[sender].balance -= totalCost(0, tx.fee.tipRate, bytesPaid)
state.accounts[sender].status = AccountStatus.DelegationUnbonding
delegation = state.delegationSet[sender]
if state.accounts[delegation.validator].status == AccountStatus.ValidatorQueued ||
state.accounts[delegation.validator].status == AccountStatus.ValidatorUnbonding ||
state.accounts[delegation.validator].status == AccountStatus.ValidatorUnbonded
validator = state.inactiveValidatorSet[delegation.validator]
else if state.accounts[delegation.validator].status == AccountStatus.ValidatorBonded
validator = state.activeValidatorSet[delegation.validator]
delegation.status = DelegationStatus.Unbonding
delegation.endEntry = validator.latestEntry
delegation.unbondingHeight = block.height + 1
validator.latestEntry += compute_new_entry(validator.pendingRewards, validator.votingPower)
validator.pendingRewards = 0
validator.delegatedCount -= 1
validator.votingPower -= delegation.stakedBalance
# Update the validator in the linked list by first removing then inserting
# Only do this if the validator is actually in the queue (i.e. bonded or queued)
if state.accounts[delegation.validator].status == AccountStatus.ValidatorBonded ||
state.accounts[delegation.validator].status == AccountStatus.ValidatorQueued
validatorQueueRemove(validator, delegation.validator)
validatorQueueInsert(validator)
state.delegationSet[sender] = delegation
if state.accounts[delegation.validator].status == AccountStatus.ValidatorQueued ||
state.accounts[delegation.validator].status == AccountStatus.ValidatorUnbonding ||
state.accounts[delegation.validator].status == AccountStatus.ValidatorUnbonded
state.inactiveValidatorSet[delegation.validator] = validator
else if state.accounts[delegation.validator].status == AccountStatus.ValidatorBonded
state.activeValidatorSet[delegation.validator] = validator
state.activeValidatorSet.activeVotingPower -= delegation.stakedBalance
state.activeValidatorSet.proposerBlockReward += tipCost(tx.fee.tipRate, bytesPaid)
SignedTransactionDataUnbondDelegation
bytesPaid = len(tx)
The following checks must be true:
tx.type==TransactionType.UnbondDelegation.totalCost(0, bytesPaid)<=state.accounts[sender].balance.tx.nonce==state.accounts[sender].nonce + 1.state.accounts[sender].status==AccountStatus.DelegationUnbonding.state.delegationSet[sender].unbondingHeight + UNBONDING_DURATION<block.height.
Apply the following to the state:
delegation = state.accounts[sender].delegationInfo
state.accounts[sender].nonce += 1
state.accounts[sender].balance -= totalCost(0, tx.fee.tipRate, bytesPaid)
state.accounts[sender].status = None
# Return the delegated stake
state.accounts[sender].balance += delegation.stakedBalance
# Also disperse rewards (commission has already been levied)
state.accounts[sender].balance += delegation.stakedBalance * (delegation.endEntry - delegation.beginEntry)
if state.accounts[delegation.validator].status == AccountStatus.ValidatorQueued ||
state.accounts[delegation.validator].status == AccountStatus.ValidatorUnbonding
state.accounts[delegation.validator].status == AccountStatus.ValidatorUnbonded
validator = state.inactiveValidatorSet[delegation.validator]
else if state.accounts[delegation.validator].status == AccountStatus.ValidatorBonded
validator = state.activeValidatorSet[delegation.validator]
if validator.delegatedCount == 0 &&
state.accounts[delegation.validator].status == AccountStatus.ValidatorUnbonded
state.accounts[delegation.validator].status = AccountStatus.None
delete state.inactiveValidatorSet[delegation.validator]
delete state.accounts[sender].delegationInfo
state.activeValidatorSet.proposerBlockReward += tipCost(tx.fee.tipRate, bytesPaid)
SignedTransactionDataBurn
bytesPaid = len(tx)
The following checks must be true:
tx.type==TransactionType.Burn.totalCost(tx.amount, bytesPaid)<=state.accounts[sender].balance.tx.nonce==state.accounts[sender].nonce + 1.
Apply the following to the state:
state.accounts[sender].nonce += 1
state.accounts[sender].balance -= totalCost(tx.amount, tx.fee.tipRate, bytesPaid)
state.activeValidatorSet.proposerBlockReward += tipCost(tx.fee.tipRate, bytesPaid)
SignedTransactionRedelegateCommission
bytesPaid = len(tx)
The following checks must be true:
tx.type==TransactionType.RedelegateCommission.totalCost(0, tx.fee.tipRate, bytesPaid)<=state.accounts[sender].balance.tx.nonce==state.accounts[sender].nonce + 1.state.accounts[tx.to].status==AccountStatus.DelegationBonded.state.accounts[sender].status==AccountStatus.ValidatorBonded.
Apply the following to the state:
state.accounts[sender].nonce += 1
state.accounts[sender].balance -= totalCost(0, tx.fee.tipRate, bytesPaid)
delegation = state.delegationSet[tx.to]
validator = state.activeValidatorSet[delegation.validator]
# Force-redelegate pending rewards for delegation
pendingRewards = delegation.stakedBalance * (validator.latestEntry - delegation.beginEntry)
delegation.stakedBalance += pendingRewards
delegation.beginEntry = validator.latestEntry
validator.latestEntry += compute_new_entry(validator.pendingRewards, validator.votingPower)
validator.pendingRewards = 0
# Assign pending commission rewards to delegation
commissionRewards = validator.commissionRewards
delegation.stakedBalance += commissionRewards
validator.commissionRewards = 0
# Update voting power
validator.votingPower += pendingRewards + commissionRewards
state.activeValidatorSet.activeVotingPower += pendingRewards + commissionRewards
state.delegationSet[tx.to] = delegation
state.activeValidatorSet[delegation.validator] = validator
state.activeValidatorSet.proposerBlockReward += tipCost(tx.fee.tipRate, bytesPaid)
SignedTransactionRedelegateReward
bytesPaid = len(tx)
The following checks must be true:
tx.type==TransactionType.RedelegateReward.totalCost(0, tx.fee.tipRate, bytesPaid)<=state.accounts[sender].balance.tx.nonce==state.accounts[sender].nonce + 1.state.accounts[sender].status==AccountStatus.DelegationBonded.state.accounts[state.delegationSet[sender].validator].status==AccountStatus.ValidatorBonded.
Apply the following to the state:
state.accounts[sender].nonce += 1
state.accounts[sender].balance -= totalCost(0, tx.fee.tipRate, bytesPaid)
delegation = state.delegationSet[sender]
validator = state.activeValidatorSet[delegation.validator]
# Redelegate pending rewards for delegation
pendingRewards = delegation.stakedBalance * (validator.latestEntry - delegation.beginEntry)
delegation.stakedBalance += pendingRewards
delegation.beginEntry = validator.latestEntry
validator.latestEntry += compute_new_entry(validator.pendingRewards, validator.votingPower)
validator.pendingRewards = 0
# Update voting power
validator.votingPower += pendingRewards
state.activeValidatorSet.activeVotingPower += pendingRewards
state.delegationSet[sender] = delegation
state.activeValidatorSet[delegation.validator] = validator
state.activeValidatorSet.proposerBlockReward += tipCost(tx.fee.tipRate, bytesPaid)
Begin Block
At the beginning of the block, rewards are distributed to the block proposer.
Apply the following to the state:
proposer = state.activeValidatorSet[block.header.proposerAddress]
# Compute block subsidy and save to state for use in end block.
rewardFactor = (TARGET_ANNUAL_ISSUANCE * BLOCK_TIME) / (SECONDS_PER_YEAR * sqrt(GENESIS_COIN_COUNT))
blockReward = rewardFactor * sqrt(state.activeValidatorSet.activeVotingPower)
state.activeValidatorSet.proposerBlockReward = blockReward
# Save proposer's initial voting power to state for use in end block.
state.activeValidatorSet.proposerInitialVotingPower = proposer.votingPower
state.activeValidatorSet[block.header.proposerAddress] = proposer
End Block
Apply the following to the state:
account = state.accounts[block.header.proposerAddress]
if account.status == AccountStatus.ValidatorUnbonding
account.status == AccountStatus.ValidatorUnbonded
proposer = state.inactiveValidatorSet[block.header.proposerAddress]
else if account.status == AccountStatus.ValidatorBonded
proposer = state.activeValidatorSet[block.header.proposerAddress]
# Flush the outstanding pending rewards.
proposer.latestEntry += compute_new_entry(proposer.pendingRewards, proposer.votingPower)
proposer.pendingRewards = 0
blockReward = state.activeValidatorSet.proposerBlockReward
commissionReward = proposer.commissionRate.numerator * blockReward // proposer.commissionRate.denominator
proposer.commissionRewards += commissionReward
proposer.pendingRewards += blockReward - commissionReward
# Even though the voting power hasn't changed yet, we consider this a period change.
proposer.latestEntry += compute_new_entry(proposer.pendingRewards, state.activeValidatorSet.proposerInitialVotingPower)
proposer.pendingRewards = 0
if account.status == AccountStatus.ValidatorUnbonding
account.status == AccountStatus.ValidatorUnbonded
state.inactiveValidatorSet[block.header.proposerAddress] = proposer
else if account.status == AccountStatus.ValidatorBonded
state.activeValidatorSet[block.header.proposerAddress] = proposer
At the end of a block, the top MAX_VALIDATORS validators by voting power with voting power greater than zero are or become active (bonded). For newly-bonded validators, the entire validator object is moved to the active validators subtree and their status is changed to bonded. For previously-bonded validators that are no longer in the top MAX_VALIDATORS validators begin unbonding.
Bonding validators is simply setting their status to AccountStatus.ValidatorBonded. The logic for validator unbonding is found in the BeginUnbondingValidator section, minus transaction sender updates (nonce, balance, and fee).
This end block implicit state transition is a single state transition, and only has a single intermediate state root associated with it.
Content Addressable Transaction Pool Specification
- 01.12.2022 | Initial specification (@cmwaters)
- 09.12.2022 | Add Push/Pull mechanics (@cmwaters)
Outline
This document specifies the properties, design and implementation of a content addressable transaction pool (CAT). This protocol is intended as an alternative to the FIFO and Priority mempools currently built-in to the Tendermint consensus protocol. The term content-addressable here, indicates that each transaction is identified by a smaller, unique tag (in this case a sha256 hash). These tags are broadcast among the transactions as a means of more compactly indicating which peers have which transactions. Tracking what each peer has aims at reducing the amount of duplication. In a network without content tracking, a peer may receive as many duplicate transactions as peers connected to. The tradeoff here therefore is that the transactions are significantly larger than the tag such that the sum of the data saved sending what would be duplicated transactions is larger than the sum of sending each peer a tag.
Purpose
The objective of such a protocol is to transport transactions from the author (usually a client) to a proposed block, optimizing both latency and throughput i.e. how quickly can a transaction be proposed (and committed) and how many transactions can be transported into a block at once.
Typically the mempool serves to receive inbound transactions via an RPC endpoint, gossip them to all nodes in the network (regardless of whether they are capable of proposing a block or not), and stage groups of transactions to both consensus and the application to be included in a block.
Assumptions
The following are assumptions inherited from existing Tendermint mempool protocols:
CheckTxshould be seen as a simple gatekeeper to what transactions enter the pool to be gossiped and staged. It is non-deterministic: one node may reject a transaction that another node keeps.- Applications implementing
CheckTxare responsible for replay protection (i.e. the same transaction being present in multiple blocks). The mempool ensures that within the same block, no duplicate transactions can exist. - The underlying p2p layer guarantees eventually reliable broadcast. A transaction need only be sent once to eventually reach the target peer.
Messages
The CAT protocol extends on the existing mempool implementations by introducing two new protobuf messages:
message SeenTx {
bytes tx_key = 1;
optional string from = 2;
}
message WantTx {
bytes tx_key = 1;
}
Both SeenTx and WantTx contain the sha256 hash of the raw transaction bytes. SeenTx also contains an optional p2p.ID that corresponds to the peer that the node received the tx from. The only validation for both is that the byte slice of the tx_key MUST have a length of 32.
Both messages are sent across a new channel with the ID: byte(0x31). This enables cross compatibility as discussed in greater detail below.
Note: The term
SeenTxis used over the more commonHasTxbecause the transaction pool contains sophisticated eviction logic. TTLs, higher priority transactions and reCheckTx may mean that a transaction pool had a transaction but does not have it any more. Semantically it's more appropriate to useSeenTxto imply not the presence of a transaction but that the node has seen it and dealt with it accordingly.
Outbound logic
A node in the protocol has two distinct modes: "broadcast" and "request/response". When a node receives a transaction via RPC (or specifically through CheckTx), it assumed that it is the only recipient from that client and thus will immediately send that transaction, after validation, to all connected peers. Afterwards, only "request/response" is used to disseminate that transaction to everyone else.
Note: Given that one can configure a mempool to switch off broadcast, there are no guarantees when a client submits a transaction via RPC and no error is returned that it will find its way into a proposers transaction pool.
A SeenTx is broadcasted to ALL nodes upon receiving a "new" transaction from a peer. The transaction pool does not need to track every unique inbound transaction, therefore "new" is identified as:
- The node does not currently have the transaction
- The node did not recently reject the transaction or has recently seen the same transaction committed (subject to the size of the cache)
- The node did not recently evict the transaction (subject to the size of the cache)
Given this criteria, it is feasible, yet unlikely that a node receives two SeenTx messages from the same peer for the same transaction.
A SeenTx MAY be sent for each transaction currently in the transaction pool when a connection with a peer is first established. This acts as a mechanism for syncing pool state across peers.
The SeenTx message MUST only be broadcasted after validation and storage. Although it is possible that a node later drops a transaction under load shedding, a SeenTx should give as strong guarantees as possible that the node can be relied upon by others that don't yet have the transaction to obtain it.
Note: Inbound transactions submitted via the RPC do not trigger a
SeenTxmessage as it is assumed that the node is the first to see the transaction and by gossiping it to others it is implied that the node has seen the transaction.
A WantTx message is always sent point to point and never broadcasted. A WantTx MUST only be sent after receiving a SeenTx message from that peer. There is one exception which is that a WantTx MAY also be sent by a node after receiving an identical WantTx message from a peer that had previously received the nodes SeenTx but which after the lapse in time, did no longer exist in the nodes transaction pool. This provides an optional synchronous method for communicating that a node no longer has a transaction rather than relying on the defaulted asynchronous approach which is to wait for a period of time and try again with a new peer.
WantTx must be tracked. A node SHOULD not send multiple WantTxs to multiple peers for the same transaction at once but wait for a period that matches the expected network latency before rerequesting the transaction to another peer.
Inbound logic
Transaction pools are solely run in-memory; thus when a node stops, all transactions are discarded. To avoid the scenario where a node restarts and does not receive transactions because other nodes recorded a SeenTx message from their previous run, each transaction pool should track peer state based per connection and not per NodeID.
Upon receiving a Txs message:
- Check whether it is in response to a request or simply an unsolicited broadcast
- Validate the tx against current resources and the applications
CheckTx - If rejected or evicted, mark accordingly
- If successful, send a
SeenTxmessage to all connected peers excluding the original sender. If it was from an initial broadcast, theSeenTxshould populate theFromfield with thep2p.IDof the recipient else if it is in response to a requestFromshould remain empty.
Upon receiving a SeenTx message:
- It should mark the peer as having seen the message.
- If the node has recently rejected that transaction, it SHOULD ignore the message.
- If the node already has the transaction, it SHOULD ignore the message.
- If the node does not have the transaction but recently evicted it, it MAY choose to rerequest the transaction if it has adequate resources now to process it.
- If the node has not seen the transaction or does not have any pending requests for that transaction, it can do one of two things:
- It MAY immediately request the tx from the peer with a
WantTx. - If the node is connected to the peer specified in
FROM, it is likely, from a non-byzantine peer, that the node will also shortly receive the transaction from the peer. It MAY wait for aTxsmessage for a bounded amount of time but MUST eventually send aWantTxmessage to either the original peer or any other peer that has the specified transaction.
- It MAY immediately request the tx from the peer with a
Upon receiving a WantTx message:
- If it has the transaction, it MUST respond with a
Txsmessage containing that transaction. - If it does not have the transaction, it MAY respond with an identical
WantTxor rely on the timeout of the peer that requested the transaction to eventually ask another peer.
Compatibility
CAT has Go API compatibility with the existing two mempool implementations. It implements both the Reactor interface required by Tendermint's P2P layer and the Mempool interface used by consensus and rpc. CAT is currently network compatible with existing implementations (by using another channel), but the protocol is unaware that it is communicating with a different mempool and that SeenTx and WantTx messages aren't reaching those peers thus it is recommended that the entire network use CAT.
Honest Block Proposer
This document describes the tasks of an honest block proposer to assemble a new block. Performing these actions is not enforced by the consensus rules, so long as a valid block is produced.
Constructing a Block
Before arranging available data into shares, the block proposer must select which transactions to include and determine the size of the original data square.
There are two restrictions on the original data's square size:
- It must be at most
AVAILABLE_DATA_ORIGINAL_SQUARE_MAX. - It must be a power of 2.
With these restrictions in mind, the block proposer performs the following actions:
- Initialize a square builder with the maximum effective square size (the lesser of the
GovMaxSquareSizegovernance parameter and theAVAILABLE_DATA_ORIGINAL_SQUARE_MAXupper bound). - Separate the available transactions from the mempool into normal transactions and blob transactions. Filter out any transactions that exceed the maximum transaction size.
- Iterate through normal transactions and attempt to add each one to the square:
- If adding the transaction would cause the total share count to exceed the maximum square capacity, skip it.
- Validate the transaction (e.g. signature verification, fee checks). If validation fails, revert the addition and skip it.
- Iterate through blob transactions and attempt to add each one to the square:
- If adding the blob transaction (including its blobs and padding required by share commitment rules) would cause the total share count to exceed the maximum square capacity, skip it.
- Validate the transaction. If validation fails, revert the addition and skip it.
- Compute the smallest square size that is a power of 2 that can fit all the accepted transactions and blobs (including any padding between blobs).
- Sort blobs by namespace (preserving the mempool-provided order of blobs within the same namespace, which is based on sender-aggregated priority).
- Write out the final square: normal transaction shares, then pay-for-blob transaction shares, then reserved padding, then blob shares (with inter-blob padding as needed), then tail padding.
Block Validity Rules
Introduction
Unlike most blockchains, Celestia derives most of its functionality from stateless commitments to data rather than stateful transitions. This means that the protocol relies heavily on block validity rules. Notably, resource constrained light clients must be able to detect when a subset of these validity rules have not been followed in order to avoid making an honest majority assumption on the consensus network. This has a significant impact on their design. More information on how light clients can check the invalidity of a block can be found in the Fraud Proofs spec.
Note Celestia relies on CometBFT (formerly tendermint) for consensus, meaning that it has single slot finality and is fork-free. Therefore, in order to ensure that an invalid block is never committed to, each validator must check that each block follows all validity rules before voting. If over two thirds of the voting power colludes to break a validity rule, then fraud proofs are created for light clients. After light clients verify fraud proofs, they halt.
Validity Rules
Before any Celestia specific validation is performed, all CometBFT block validation rules must be followed.
Notably, this includes verifying data availability. Consensus nodes verify data availability by simply downloading the entire block.
Note Light clients only sample a fraction of the block. More details on how sampling actually works can be found in the seminal "Fraud and Data Availability Proofs: Maximising Light Client Security and Scaling Blockchains with Dishonest Majorities" and in the
celestia-noderepo.
Celestia specific validity rules can be categorized into multiple groups:
Block Rules
- In
Block.Data.Txs, allBlobTxtransactions must be ordered after non-BlobTxtransactions.
Transaction Validity Rules
App Version 1
There is no validity rule that transactions must be decodable so the following rules only apply to transactions that are decodable.
- Decodable transactions must pass all AnteHandler checks.
- Decodable non-
BlobTxtransactions must not contain aMsgPayForBlobsmessage. - Decodable
BlobTxtransactions must be valid according to the BlobTx validity rules.
App Version 2
- All transactions must be decodable.
- All transactions must pass all AnteHandler checks.
- Non-
BlobTxtransactions must not contain aMsgPayForBlobsmessage. BlobTxtransactions must be valid according to the BlobTx validity rules.
Data Root Construction
The data root must be calculated from a correctly constructed data square per the data square layout rules.
AnteHandler
Celestia makes use of a Cosmos SDK AnteHandler in order to reject decodable sdk.Txs that do not meet certain criteria. The AnteHandler is invoked at multiple times during the transaction lifecycle:
CheckTxprior to the transaction entering the mempoolPrepareProposalwhen the block proposer includes the transaction in a block proposalProcessProposalwhen validators validate the transaction in a block proposalDeliverTxwhen full nodes execute the transaction in a decided block
The AnteHandler is defined in app/ante/ante.go. The app version impacts AnteHandler behavior. See:
- AnteHandler v1
- AnteHandler v2
- AnteHandler v3
- AnteHandler v4
- AnteHandler v5
- AnteHandler v6
- AnteHandler v7
AnteHandler v1
The AnteHandler chains together several decorators to ensure the following criteria are met for app version 1:
- The tx does not contain any extension options.
- The tx passes
ValidateBasic(). - The tx's timeout_height has not been reached if one is specified.
- The tx's memo is <= the max memo characters where
MaxMemoCharacters = 256. - The tx's gas_limit is > the gas consumed based on the tx's size where
TxSizeCostPerByte = 10. - The tx's feepayer has enough funds to pay fees for the tx. The tx's feepayer is the feegranter (if specified) or the tx's first signer. Note the feegrant module is enabled.
- The tx's count of signatures <= the max number of signatures. The max number of signatures is
TxSigLimit = 7. - The tx's gas_limit is > the gas consumed based on the tx's signatures.
- The tx's signatures are valid. For each signature, ensure that the signature's sequence number (a.k.a nonce) matches the account sequence number of the signer.
- The tx's gas_limit is > the gas consumed based on the blob size(s). Since blobs are charged based on the number of shares they occupy, the gas consumed is calculated as follows:
gasToConsume = sharesNeeded(blob) * bytesPerShare * gasPerBlobByte. WherebytesPerShareis a global constant (an alias forShareSize = 512) andgasPerBlobByteis a governance parameter that can be modified (theDefaultGasPerBlobByte = 8). - The tx's total blob size is <= the max blob size. The max blob size is derived from the maximum valid square size. The max valid square size is the minimum of:
GovMaxSquareSizeandSquareSizeUpperBound. - The tx does not contain a message of type MsgSubmitProposal with zero proposal messages.
- The tx is not an IBC packet or update message that has already been processed.
In addition to the above criteria, the AnteHandler also has a number of side-effects:
- Tx fees are deducted from the tx's feepayer and added to the fee collector module account.
- Tx priority is calculated based on the smallest denomination of gas price in the tx and set in context.
- The nonce of all tx signers is incremented by 1.
AnteHandler v2
The AnteHandler chains together several decorators to ensure the following criteria are met for app version 2:
- The tx does not contain any messages that are unsupported by the current app version. See
MsgVersioningGateKeeper. - The tx does not contain any extension options.
- The tx passes
ValidateBasic(). - The tx's timeout_height has not been reached if one is specified.
- The tx's memo is <= the max memo characters where
MaxMemoCharacters = 256. - The tx's gas_limit is > the gas consumed based on the tx's size where
TxSizeCostPerByte = 10. - The tx's feepayer has enough funds to pay fees for the tx. The tx's feepayer is the feegranter (if specified) or the tx's first signer. Note the feegrant module is enabled.
- The tx's gas price is >= the network minimum gas price where
NetworkMinGasPrice = 0.000001utia. - The tx's count of signatures <= the max number of signatures. The max number of signatures is
TxSigLimit = 7. - The tx's gas_limit is > the gas consumed based on the tx's signatures.
- The tx's signatures are valid. For each signature, ensure that the signature's sequence number (a.k.a nonce) matches the account sequence number of the signer.
- The tx's gas_limit is > the gas consumed based on the blob size(s). Since blobs are charged based on the number of shares they occupy, the gas consumed is calculated as follows:
gasToConsume = sharesNeeded(blob) * bytesPerShare * gasPerBlobByte. WherebytesPerShareis a global constant (an alias forShareSize = 512) andgasPerBlobByteis a governance parameter that can be modified (theDefaultGasPerBlobByte = 8). - The tx's total blob share count is <= the max blob share count. The max blob share count is derived from the maximum valid square size. The max valid square size is the minimum of:
GovMaxSquareSizeandSquareSizeUpperBound. - The tx does not contain a message of type MsgSubmitProposal with zero proposal messages.
- The tx is not an IBC packet or update message that has already been processed.
In addition to the above criteria, the AnteHandler also has a number of side-effects:
- Tx fees are deducted from the tx's feepayer and added to the fee collector module account.
- Tx priority is calculated based on the smallest denomination of gas price in the tx and set in context.
- The nonce of all tx signers is incremented by 1.
AnteHandler v3
The AnteHandler chains together several decorators to ensure the following criteria are met for app version 3:
- The tx does not contain any messages that are unsupported by the current app version. See
MsgVersioningGateKeeper. - The
sdk.Txsize is not larger than the application's configured versioned constant MaxTxSize. This limit does not apply to blobs. - The tx does not contain any extension options.
- The tx passes
ValidateBasic(). - The tx's timeout_height has not been reached if one is specified.
- The tx's memo is <= the max memo characters where
MaxMemoCharacters = 256. - The tx's gas_limit is > the gas consumed based on the tx's size where
TxSizeCostPerByte = 10. - The tx's feepayer has enough funds to pay fees for the tx. The tx's feepayer is the feegranter (if specified) or the tx's first signer. Note the feegrant module is enabled.
- The tx's gas price is >= the network minimum gas price where
NetworkMinGasPrice = 0.000001utia. - The tx's count of signatures <= the max number of signatures. The max number of signatures is
TxSigLimit = 7. - The tx's gas_limit is > the gas consumed based on the tx's signatures.
- The tx's signatures are valid. For each signature, ensure that the signature's sequence number (a.k.a nonce) matches the account sequence number of the signer.
- The tx does not contain a
MsgExecwith a nestedMsgExecorMsgPayForBlobs. - The tx's gas_limit is > the gas consumed based on the blob size(s). Since blobs are charged based on the number of shares they occupy, the gas consumed is calculated as follows:
gasToConsume = sharesNeeded(blob) * bytesPerShare * gasPerBlobByte. WherebytesPerShareis a global constant (an alias forShareSize = 512) andgasPerBlobByteis a versioned constant that can be modified through hard forks (theDefaultGasPerBlobByte = 8). - The tx's total blob share count is <= the max blob share count. The max blob share count is derived from the maximum valid square size. The max valid square size is the minimum of:
GovMaxSquareSizeandSquareSizeUpperBound. - The tx does not contain a message of type MsgSubmitProposal with zero proposal messages.
- The tx is not an IBC packet or update message that has already been processed.
In addition to the above criteria, the AnteHandler also has a number of side-effects:
- Tx fees are deducted from the tx's feepayer and added to the fee collector module account.
- Tx priority is calculated based on the smallest denomination of gas price in the tx and set in context.
- The nonce of all tx signers is incremented by 1.
AnteHandler v4
The AnteHandler chains together several decorators to ensure the following criteria are met for app version 4:
- The tx does not contain any extension options.
- The tx passes
ValidateBasic(). - The tx's timeout_height has not been reached if one is specified.
- The tx's memo is <= the max memo characters where
MaxMemoCharacters = 256. - The tx's gas_limit is > the gas consumed based on the tx's size where
TxSizeCostPerByte = 10. - The tx's feepayer has enough funds to pay fees for the tx. The tx's feepayer is the feegranter (if specified) or the tx's first signer. Note the feegrant module is enabled.
- The tx's gas price is >= the network minimum gas price where
NetworkMinGasPrice = 0.000001utia. - The tx's count of signatures <= the max number of signatures. The max number of signatures is
TxSigLimit = 7. - The tx's gas_limit is > the gas consumed based on the tx's signatures.
- The tx's signatures are valid. For each signature, ensure that the signature's sequence number (a.k.a nonce) matches the account sequence number of the signer.
- The tx does not contain a
MsgExecwith a nestedMsgExecorMsgPayForBlobs. - The tx's gas_limit is > the gas consumed based on the blob size(s). Since blobs are charged based on the number of shares they occupy, the gas consumed is calculated as follows:
gasToConsume = sharesNeeded(blob) * bytesPerShare * gasPerBlobByte. WherebytesPerShareis a global constant (an alias forShareSize = 512) andgasPerBlobByteis a versioned constant that can be modified through hard forks (theDefaultGasPerBlobByte = 8). - The tx's total blob share count is <= the max blob share count. The max blob share count is derived from the maximum valid square size. The max valid square size is the minimum of:
GovMaxSquareSizeandSquareSizeUpperBound. - The tx does not contain a message of type MsgSubmitProposal with zero proposal messages or with a proposal message that modifies a parameter that is not governance modifiable.
- The tx is not an IBC packet or update message that has already been processed.
- The tx does not contain any messages that are disabled by the circuit breaker (e.g.
MsgSoftwareUpgrade,MsgCancelUpgrade,MsgIBCSoftwareUpgrade).
In addition to the above criteria, the AnteHandler also has a number of side-effects:
- Tx fees are deducted from the tx's feepayer and added to the fee collector module account.
- Tx priority is calculated based on the smallest denomination of gas price in the tx and set in context.
- The nonce of all tx signers is incremented by 1.
AnteHandler v5
The AnteHandler chains together several decorators to ensure the following criteria are met for app version 5:
- The tx does not contain any extension options.
- The tx passes
ValidateBasic(). - The tx's timeout_height has not been reached if one is specified.
- The tx's memo is <= the max memo characters where
MaxMemoCharacters = 256. - The tx's gas_limit is > the gas consumed based on the tx's size where
TxSizeCostPerByte = 10. - The tx's feepayer has enough funds to pay fees for the tx. The tx's feepayer is the feegranter (if specified) or the tx's first signer. Note the feegrant module is enabled.
- The tx's gas price is >= the network minimum gas price where
NetworkMinGasPrice = 0.000001utia. - The tx's count of signatures <= the max number of signatures. The max number of signatures is
TxSigLimit = 7. - The tx's gas_limit is > the gas consumed based on the tx's signatures.
- The tx's signatures are valid. For each signature, ensure that the signature's sequence number (a.k.a nonce) matches the account sequence number of the signer.
- The tx does not contain a
MsgExecwith a nestedMsgExecorMsgPayForBlobs. - The tx's gas_limit is > the gas consumed based on the blob size(s). Since blobs are charged based on the number of shares they occupy, the gas consumed is calculated as follows:
gasToConsume = sharesNeeded(blob) * bytesPerShare * gasPerBlobByte. WherebytesPerShareis a global constant (an alias forShareSize = 512) andgasPerBlobByteis a versioned constant that can be modified through hard forks (theDefaultGasPerBlobByte = 8). - The tx's total blob share count is <= the max blob share count. The max blob share count is derived from the maximum valid square size. The max valid square size is the minimum of:
GovMaxSquareSizeandSquareSizeUpperBound. - The tx does not contain a message of type MsgSubmitProposal with zero proposal messages or with a proposal message that modifies a parameter that is not governance modifiable.
- The tx is not an IBC packet or update message that has already been processed.
- The tx does not contain any messages that are disabled by the circuit breaker (e.g.
MsgSoftwareUpgrade,MsgCancelUpgrade,MsgIBCSoftwareUpgrade).
In addition to the above criteria, the AnteHandler also has a number of side-effects:
- Tx fees are deducted from the tx's feepayer and added to the fee collector module account.
- Tx priority is calculated based on the smallest denomination of gas price in the tx and set in context.
- The nonce of all tx signers is incremented by 1.
AnteHandler v6
The AnteHandler chains together several decorators to ensure the following criteria are met for app version 6:
- Panics are wrapped with the transaction string format for better error reporting.
- A gas meter is set up in the context before any gas consumption occurs.
- The tx does not contain any messages that are disabled by the circuit breaker (e.g.
MsgSoftwareUpgrade,MsgCancelUpgrade,MsgIBCSoftwareUpgrade). - The tx does not contain any extension options.
- The tx passes
ValidateBasic(). - The tx's timeout_height has not been reached if one is specified.
- The tx's memo is <= the max memo characters where
MaxMemoCharacters = 256. - The tx's gas_limit is > the gas consumed based on the tx's size where
TxSizeCostPerByte = 10. - The tx's feepayer has enough funds to pay fees for the tx. The tx's feepayer is the feegranter (if specified) or the tx's first signer. Note the feegrant module is enabled.
- The tx's gas price is >= the network minimum gas price where
NetworkMinGasPrice = 0.000001utia. - Public keys are set in the context for the fee-payer and all signers.
- The tx's count of signatures <= the max number of signatures. The max number of signatures is
TxSigLimit = 7. - The tx's gas_limit is > the gas consumed based on the tx's signatures.
- The tx's signatures are valid. For each signature, ensure that the signature's sequence number (a.k.a nonce) matches the account sequence number of the signer.
- The tx does not contain a
MsgExecwith a nestedMsgExecorMsgPayForBlobs. - The tx's gas_limit is > the gas consumed based on the blob size(s). Since blobs are charged based on the number of shares they occupy, the gas consumed is calculated as follows:
gasToConsume = sharesNeeded(blob) * bytesPerShare * gasPerBlobByte. WherebytesPerShareis a global constant (an alias forShareSize = 512) from the go-square package andgasPerBlobByteis a versioned constant that can be modified through hard forks (theGasPerBlobByte = 8). - The tx's total blob share count is <= the max blob share count. The max blob share count is derived from the maximum valid square size. The max valid square size is the minimum of:
GovMaxSquareSizeandSquareSizeUpperBound. - The tx does not contain a message of type MsgSubmitProposal with zero proposal messages or with a proposal message that modifies a parameter that is not governance modifiable.
- The tx is not an IBC packet or update message that has already been processed.
In addition to the above criteria, the AnteHandler also has a number of side-effects:
- Tx fees are deducted from the tx's feepayer and added to the fee collector module account.
- Tx priority is calculated based on the smallest denomination of gas price in the tx and set in context.
- The nonce of all tx signers is incremented by 1.
AnteHandler v7
The AnteHandler chains together several decorators to ensure the following criteria are met for app version 7:
- Panics are wrapped with the transaction string format for better error reporting.
- A gas meter is set up in the context before any gas consumption occurs.
- The tx does not contain any messages that are disabled by the circuit breaker (e.g.
MsgSoftwareUpgrade,MsgCancelUpgrade,MsgIBCSoftwareUpgrade). - The tx does not contain any extension options.
- The tx passes
ValidateBasic(). - The tx's timeout_height has not been reached if one is specified.
- The tx's memo is <= the max memo characters where
MaxMemoCharacters = 256. - The tx's gas_limit is > the gas consumed based on the tx's size where
TxSizeCostPerByte = 10. - The tx's feepayer has enough funds to pay fees for the tx. The tx's feepayer is the feegranter (if specified) or the tx's first signer. Note the feegrant module is enabled.
- The tx's gas price is >= the network minimum gas price where
NetworkMinGasPrice = 0.000001utia. - Public keys are set in the context for the fee-payer and all signers.
- The tx's count of signatures <= the max number of signatures. The max number of signatures is
TxSigLimit = 7. - The tx's gas_limit is > the gas consumed based on the tx's signatures.
- The tx's signatures are valid. For each signature, ensure that the signature's sequence number (a.k.a nonce) matches the account sequence number of the signer.
- The tx does not contain a
MsgExecwith a nestedMsgExecorMsgPayForBlobs. - The tx's gas_limit is > the gas consumed based on the blob size(s). Since blobs are charged based on the number of shares they occupy, the gas consumed is calculated as follows:
gasToConsume = sharesNeeded(blob) * bytesPerShare * gasPerBlobByte. WherebytesPerShareis a global constant (an alias forShareSize = 512) from the go-square package andgasPerBlobByteis a versioned constant that can be modified through hard forks (theGasPerBlobByte = 8). - The tx's total blob share count is <= the max blob share count. The max blob share count is derived from the maximum valid square size. The max valid square size is the minimum of:
GovMaxSquareSizeandSquareSizeUpperBound. - The tx does not contain a message of type MsgSubmitProposal with zero proposal messages or with a proposal message that modifies a parameter that is not governance modifiable.
- The tx is not an IBC packet or update message that has already been processed.
In addition to the above criteria, the AnteHandler also has a number of side-effects:
- Tx fees are deducted from the tx's feepayer and added to the fee collector module account.
- Tx priority is calculated based on the smallest denomination of gas price in the tx and set in context.
- The nonce of all tx signers is incremented by 1.
Fraud Proofs
Bad Encoding Fraud Proofs
In order for data availability sampling to work, light clients must be convinced that erasure encoded parity data was encoded correctly. For light clients, this is ultimately enforced via bad encoding fraud proofs (BEFPs). Consensus nodes must verify this themselves before considering a block valid. This is done automatically by verifying the data root of the header, since that requires reconstructing the square from the block data, performing the erasure encoding, calculating the data root using that representation, and then comparing the data root found in the header.
Blob Inclusion
TODO
State
State fraud proofs allow light clients to avoid making an honest majority assumption for state validity. While these are not incorporated into the protocol as of v1.0.0, there are example implementations that can be found in Rollkit. More info in rollkit-ADR009.
Networking
Wire Format
AvailableData
| name | type | description |
|---|---|---|
availableDataRows | AvailableDataRow[] | List of rows. |
AvailableDataRow
| name | type | description |
|---|---|---|
shares | Share[] | Shares in a row. |
Invalid Erasure Coding
If a malicious block producer incorrectly computes the 2D Reed-Solomon code for a block's data, a fraud proof for this can be presented. We assume that the light clients have the AvailableDataHeader and the Header for each block. Hence, given a ShareProof, they can verify if the rowRoot or colRoot specified by isCol and position commits to the corresponding Share. Similarly, given the height of a block, they can access all elements within the AvailableDataHeader and the Header of the block.
ShareProof
| name | type | description |
|---|---|---|
share | Share | The share. |
proof | NamespaceMerkleTreeInclusionProof | The Merkle proof of the share in the offending row or column root. |
isCol | bool | A Boolean indicating if the proof is from a row root or column root; false if it is a row root. |
position | uint64 | The index of the share in the offending row or column. |
Invalid State Update
If a malicious block producer incorrectly computes the state, a fraud proof for this can be presented. We assume that the light clients have the AvailableDataHeader and the Header for each block. Hence, given a ShareProof, they can verify if the rowRoot or colRoot specified by isCol and position commits to the corresponding Share. Similarly, given the height of a block, they can access all elements within the AvailableDataHeader and the Header of the block.
Public-Key Cryptography
Consensus-critical data is authenticated using ECDSA with the curves: Secp256k1 or Ed25519.
Secp256k1
The Secp256k1 key type is used by accounts that submit transactions to be included in Celestia.
Libraries
A highly-optimized library is available in C (https://github.com/bitcoin-core/secp256k1), with wrappers in Go (https://pkg.go.dev/github.com/ethereum/go-ethereum/crypto/secp256k1) and Rust (https://docs.rs/crate/secp256k1).
Public-keys
Secp256k1 public keys can be compressed to 257-bits (or 33 bytes) per the format described in the Cosmos SDK accounts documentation.
Addresses
Cosmos addresses are 20 bytes in length.
Signatures
Deterministic signatures (RFC-6979) should be used when signing, but this is not enforced at the protocol level as it cannot be for Secp256k1 signatures.
Signatures are represented as the r and s (each 32 bytes) values of the signature. r and s take on their usual meaning (see: SEC 1, 4.1.3 Signing Operation). Signatures are encoded with protobuf as described in the encoding documentation.
Human Readable Encoding
In front-ends addresses are prefixed with the Bech32 prefix celestia. For example, a valid address is celestia1kj39jkzqlr073t42am9d8pd40tgudc3e2kj9yf.
Ed25519
The Ed25519 key type is used by validators.
Libraries
Public Keys
Ed25519 public keys are 32 bytes in length. They often appear in validator configuration files (e.g. genesis.json) base64 encoded:
"pub_key": {
"type": "tendermint/PubKeyEd25519",
"value": "DMEMMj1+thrkUCGocbvvKzXeaAtRslvX9MWtB+smuIA="
}
Addresses
Ed25519 addresses are the first 20-bytes of the SHA256 hash of the raw 32-byte public key:
address = SHA256(pubkey)[:20]
Signatures
Ed25519 signatures are 64 bytes in length.
Data Square Layout
Preamble
Celestia uses a data availability scheme that allows nodes to determine whether a block's data was published without downloading the whole block. The core of this scheme is arranging data in a two-dimensional matrix of shares, then applying erasure coding to each row and column. This document describes the rationale for how data—transactions, blobs, and other data—is actually arranged. Familiarity with the originally proposed data layout format is assumed.
Layout Rationale
Block data consists of:
- Standard cosmos-SDK transactions: (which are often represented internally as the
sdk.Txinterface) as described in cosmos-sdk ADR020- These transactions contain protobuf encoded
sdk.Msgs, which get executed atomically (if one fails they all fail) to update the Celestia state. The complete list of modules, which define thesdk.Msgs that the state machine is capable of handling, can be found in the state machine modules spec. Examples include standard cosmos-sdk module messages such as MsgSend, and celestia specific module messages such asMsgPayForBlobs
- These transactions contain protobuf encoded
- Blobs: binary large objects which do not modify the Celestia state, but which are intended for a Celestia application identified with a provided namespace.
We want to arrange this data into a k * k matrix of fixed-sized shares, which will later be committed to in Namespace Merkle Trees (NMTs) so that individual shares in this matrix can be proven to belong to a single data root. k must always be a power of 2 (e.g. 1, 2, 4, 8, 16, 32, etc.) as this is optimal for the erasure coding algorithm.
The simplest way we can imagine arranging block data is to simply serialize it all in no particular order, split it into fixed-sized shares, then arrange those shares into the k * k matrix in row-major order. However, this naive scheme can be improved in a number of ways, described below.
First, we impose some ground rules:
- Data must be ordered by namespace. This makes queries into a NMT commitment of that data more efficient.
- Since non-blob data are not naturally intended for particular namespaces, we assign reserved namespaces for them. A range of namespaces is reserved for this purpose, starting from the lowest possible namespace.
- By construction, the above two rules mean that non-blob data always precedes blob data in the row-major matrix, even when considering single rows or columns.
- Data with different namespaces must not be in the same share. This might cause a small amount of wasted block space, but makes the NMT easier to reason about in general since leaves are guaranteed to belong to a single namespace.
Given these rules, a square may look as follows:
Padding is addressed in the padding section. Namespace C contains two blobs of two shares each while Namespace D contains one blob of three shares.
Ordering
The order of blobs in a namespace is determined by the order that transactions are provided to PrepareProposal, which is the order they are reaped from the mempool. The CAT mempool groups transactions by signer and orders these groups by a gas-weighted average priority (where priority is derived from the gas-price = fee/gas). Within a signer's group, transactions are ordered by sequence number. As a result, blobs from a higher-priority signer group generally appear before blobs from a lower-priority group within the same namespace. However, this is not strict per-transaction priority ordering: if a single signer has transactions with varying gas prices, the averaging can cause a high-priority transaction to appear after a lower-priority transaction from a different signer (see celestia-core CAT mempool for details).
Blob Share Commitment Rules
Transactions can pay fees for a blob to be included in the same block as the transaction itself. It may seem natural to bundle the MsgPayForBlobs transaction that pays for a number of blobs with these blobs (which is the case in other blockchains with native execution, e.g. calldata in Ethereum transactions or OP_RETURN data in Bitcoin transactions), however this would mean that processes validating the state of the Celestia network would need to download all blob data. PayForBlob transactions must therefore only include a commitment to (i.e. some hash of) the blob they pay fees for. If implemented naively (e.g. with a simple hash of the blob, or a simple binary Merkle tree root of the blob), this can lead to a data availability problem, as there are no guarantees that the data behind these commitments is actually part of the block data.
To that end, we impose some additional rules onto blobs only: blobs must be placed in a way such that both the transaction sender and the block producer can be held accountable—a necessary property for e.g. fee burning. Accountable in this context means that
- The transaction sender must pay sufficient fees for blob inclusion.
- The block proposer cannot claim that a blob was included when it was not (which implies that a transaction and the blob it pays for must be included in the same block). In addition all blobs must be accompanied by a PayForBlob transaction.
Specifically, a MsgPayForBlobs must include a ShareCommitment over the contents of each blob it is paying for. If the transaction sender knows 1) k, the size of the matrix, 2) the starting location of their blob in a row, and 3) the length of the blob (they know this since they are sending the blob), then they can actually compute a sequence of roots to subtrees in the row NMTs. Taking the simple Merkle root of these subtree roots provides us with the ShareCommitment that gets included in MsgPayForBlobs. Using subtree roots instead of all the leaves makes blob inclusion proofs smaller.
Understanding 1) and 2) would usually require interaction with the block proposer. To make the possible starting locations of blobs sufficiently predictable and to make ShareCommitment independent of k, we impose an additional rule. The blob must start at a multiple of the SubtreeWidth.
The SubtreeWidth is calculated as the length of the blob in shares, divided by the SubtreeRootThreshold and rounded up to the nearest power of 2 (implementation here). If the output is greater than the minimum square size that the blob can fit in (i.e. a blob of 15 shares has a minimum square size of 4) then we take that minimum value. This SubtreeWidth is used as the width of the first mountain in the Merkle Mountain Range that would all together represent the ShareCommitment over the blob.
The SubtreeRootThreshold is an arbitrary versioned protocol constant that aims to put a soft limit on the number of subtree roots included in a blob inclusion proof, as described in ADR013. A higher SubtreeRootThreshold means less padding and more tightly packed squares but also means greater blob inclusion proof sizes.
With the above constraint, we can compute subtree roots deterministically. For example, a blob of 172 shares and SubtreeRootThreshold (SRT) = 64, must start on a share index that is a multiple of 4 because 172/64 = 3. 3 rounded up to the nearest power of 2 is 4. In this case, there will be a maximum of 3 shares of padding between blobs (more on padding below). The maximum subtree width in shares for the first mountain in the Merkle range will be 4 (The actual mountain range would be 43 subtree roots of 4 shares each). The ShareCommitment is then the Merkle tree over the peaks of the mountain range.
Padding
Given these rules whereby blobs in their share format can't be directly appended one after the other, we use padding shares to fill the gaps. These are shares with a particular format (see padding). Padding always comes after all the blobs in the namespace. The padding at the end of the reserved namespace and at the end of the square are special in that they belong to unique namespaces. All other padding shares use the namespace of the blob before it in the data square.
Resource Pricing
For all standard cosmos-sdk transactions (staking, IBC, etc), Celestia utilizes the default cosmos-sdk mechanisms for pricing resources. This involves incrementing a gas counter during transaction execution each time the state is read from/written to, or when specific costly operations occur such as signature verification or inclusion of data.
// GasMeter interface to track gas consumption
type GasMeter interface {
GasConsumed() Gas
GasConsumedToLimit() Gas
GasRemaining() Gas
Limit() Gas
ConsumeGas(amount Gas, descriptor string)
RefundGas(amount Gas, descriptor string)
IsPastLimit() bool
IsOutOfGas() bool
String() string
}
We can see how this gas meter is used in practice by looking at the store. Notice where gas is consumed each time we write or read, specifically a flat cost for initiating the action followed by a prorated cost for the amount of data read or written.
// Implements KVStore.
func (gs *Store) Get(key []byte) (value []byte) {
gs.gasMeter.ConsumeGas(gs.gasConfig.ReadCostFlat, types.GasReadCostFlatDesc)
value = gs.parent.Get(key)
// TODO overflow-safe math?
gs.gasMeter.ConsumeGas(gs.gasConfig.ReadCostPerByte*types.Gas(len(key)), types.GasReadPerByteDesc)
gs.gasMeter.ConsumeGas(gs.gasConfig.ReadCostPerByte*types.Gas(len(value)), types.GasReadPerByteDesc)
return value
}
// Implements KVStore.
func (gs *Store) Set(key []byte, value []byte) {
types.AssertValidKey(key)
types.AssertValidValue(value)
gs.gasMeter.ConsumeGas(gs.gasConfig.WriteCostFlat, types.GasWriteCostFlatDesc)
// TODO overflow-safe math?
gs.gasMeter.ConsumeGas(gs.gasConfig.WriteCostPerByte*types.Gas(len(key)), types.GasWritePerByteDesc)
gs.gasMeter.ConsumeGas(gs.gasConfig.WriteCostPerByte*types.Gas(len(value)), types.GasWritePerByteDesc)
gs.parent.Set(key, value)
}
The configuration for the gas meter used by Celestia is as follows.
// KVGasConfig returns a default gas config for KVStores.
func KVGasConfig() GasConfig {
return GasConfig{
HasCost: 1000,
DeleteCost: 1000,
ReadCostFlat: 1000,
ReadCostPerByte: 3,
WriteCostFlat: 2000,
WriteCostPerByte: 30,
IterNextCostFlat: 30,
}
}
// TransientGasConfig returns a default gas config for TransientStores.
func TransientGasConfig() GasConfig {
return GasConfig{
HasCost: 100,
DeleteCost: 100,
ReadCostFlat: 100,
ReadCostPerByte: 0,
WriteCostFlat: 200,
WriteCostPerByte: 3,
IterNextCostFlat: 3,
}
}
Two notable gas consumption events that are not Celestia specific are the total bytes used for a transaction and the verification of the signature
func (cgts ConsumeTxSizeGasDecorator) AnteHandle(ctx sdk.Context, tx sdk.Tx, simulate bool, next sdk.AnteHandler) (sdk.Context, error) {
sigTx, ok := tx.(authsigning.SigVerifiableTx)
if !ok {
return ctx, sdkerrors.Wrap(sdkerrors.ErrTxDecode, "invalid tx type")
}
params := cgts.ak.GetParams(ctx)
ctx.GasMeter().ConsumeGas(params.TxSizeCostPerByte*sdk.Gas(len(ctx.TxBytes())), "txSize")
...
}
// DefaultSigVerificationGasConsumer is the default implementation of SignatureVerificationGasConsumer. It consumes gas
// for signature verification based upon the public key type. The cost is fetched from the given params and is matched
// by the concrete type.
func DefaultSigVerificationGasConsumer(
meter sdk.GasMeter, sig signing.SignatureV2, params types.Params,
) error {
pubkey := sig.PubKey
switch pubkey := pubkey.(type) {
case *ed25519.PubKey:
meter.ConsumeGas(params.SigVerifyCostED25519, "ante verify: ed25519")
return sdkerrors.Wrap(sdkerrors.ErrInvalidPubKey, "ED25519 public keys are unsupported")
case *secp256k1.PubKey:
meter.ConsumeGas(params.SigVerifyCostSecp256k1, "ante verify: secp256k1")
return nil
case *secp256r1.PubKey:
meter.ConsumeGas(params.SigVerifyCostSecp256r1(), "ante verify: secp256r1")
return nil
case multisig.PubKey:
multisignature, ok := sig.Data.(*signing.MultiSignatureData)
if !ok {
return fmt.Errorf("expected %T, got, %T", &signing.MultiSignatureData{}, sig.Data)
}
err := ConsumeMultisignatureVerificationGas(meter, multisignature, pubkey, params, sig.Sequence)
if err != nil {
return err
}
return nil
default:
return sdkerrors.Wrapf(sdkerrors.ErrInvalidPubKey, "unrecognized public key type: %T", pubkey)
}
}
Since gas is consumed in this fashion and many of the cosmos-sdk transactions are composable, any given transaction can have a large window of possible gas consumption. For example, vesting accounts use more bytes of state than a normal account, so more gas is consumed each time a vesting account is read from or updated.
Parameters
There are four parameters that can be modified via governance to modify gas usage.
| Parameter | Default Value | Description | Changeable via Governance |
|---|---|---|---|
| consensus/max_gas | -1 | The maximum gas allowed in a block. Default of -1 means this value is not capped. | True |
| auth/tx_size_cost_per_byte | 10 | Gas used per each byte used by the transaction. | True |
| auth/sig_verify_cost_secp256k1 | 1000 | Gas used per verifying a secp256k1 signature | True |
| blob/gas_per_blob_byte | 8 | Gas used per byte used by blob. Note that this value is applied to all encoding overhead, meaning things like the padding of the remaining share and namespace. See PFB gas estimation section for more details. | True |
Gas Limit
The gas limit must be included in each transaction. If the transaction exceeds this gas limit during the execution of the transaction, then the transaction will fail.
Note: When a transaction is submitted to the mempool, the transaction is not fully executed. This can lead to a transaction getting accepted by the mempool and eventually included in a block, yet failing because the transaction ends up exceeding the gas limit.
Fees are not currently refunded. While users can specify a gas price, the total fee is then calculated by simply multiplying the gas limit by the gas price. The entire fee is then deducted from the transaction no matter what.
Fee market
By default, Celestia's consensus nodes prioritize transactions in their mempools
based on gas price. In version 1, there was no enforced minimum gas price, which
allowed each consensus node to independently set its own minimum gas price in
app.toml. This even permitted a gas price of 0, thereby creating the
possibility of secondary markets. In version 2, Celestia introduces a network
minimum gas price, a consensus constant, unaffected by individual node
configurations. Although nodes retain the freedom to increase gas prices
locally, all transactions in a block must be greater than or equal to the network
minimum threshold. If a block is proposed that contains a tx with a gas price
below the network min gas price, the block will be rejected as invalid.
Estimating PFB cost
Generally, the gas used by a PFB transaction involves a static "fixed cost" and a dynamic cost based on the size of each blob involved in the transaction.
Note: For a general use case of a normal account submitting a PFB, the static costs can be treated as such. However, due to the description above of how gas works in the cosmos-sdk this is not always the case. Notably, if we use a vesting account or the
feegrantmodules, then these static costs change.
The "fixed cost" is an approximation of the gas consumed by operations outside
the function GasToConsume (for example, signature verification, tx size, read
access to accounts), which has a default value of 65,000.
Note: the first transaction sent by an account (sequence number == 0) has an additional one time gas cost of 10,000. If this is the case, this should be accounted for.
Each blob in the PFB contributes to the total gas cost based on its size. The
function GasToConsume calculates the total gas consumed by all the blobs
involved in a PFB, where each blob's gas cost is computed by first determining
how many shares are needed to store the blob size. Then, it computes the product
of the number of shares, the number of bytes per share, and the gasPerByte
parameter. Finally, it adds a static amount per blob.
The gas cost per blob byte and gas cost per transaction byte are parameters that could potentially be adjusted through the system's governance mechanisms. Hence, actual costs may vary depending on the current settings of these parameters.
Tracing Gas Consumption
This figure plots each instance of the gas meter being incremented as a colored dot over the execution lifecycle of a given transaction. The y-axis is units of gas and the x-axis is cumulative gas consumption. The legend shows which color indicates what the cause of the gas consumption was.
This code used to trace gas consumption can be found in the tools/gasmonitor of the branch for #2131, and the script to generate the plots below can be found in this gist (warning: this script will not be maintained).
MsgSend
Here we can see the gas consumption trace of a common send transaction for
1utia
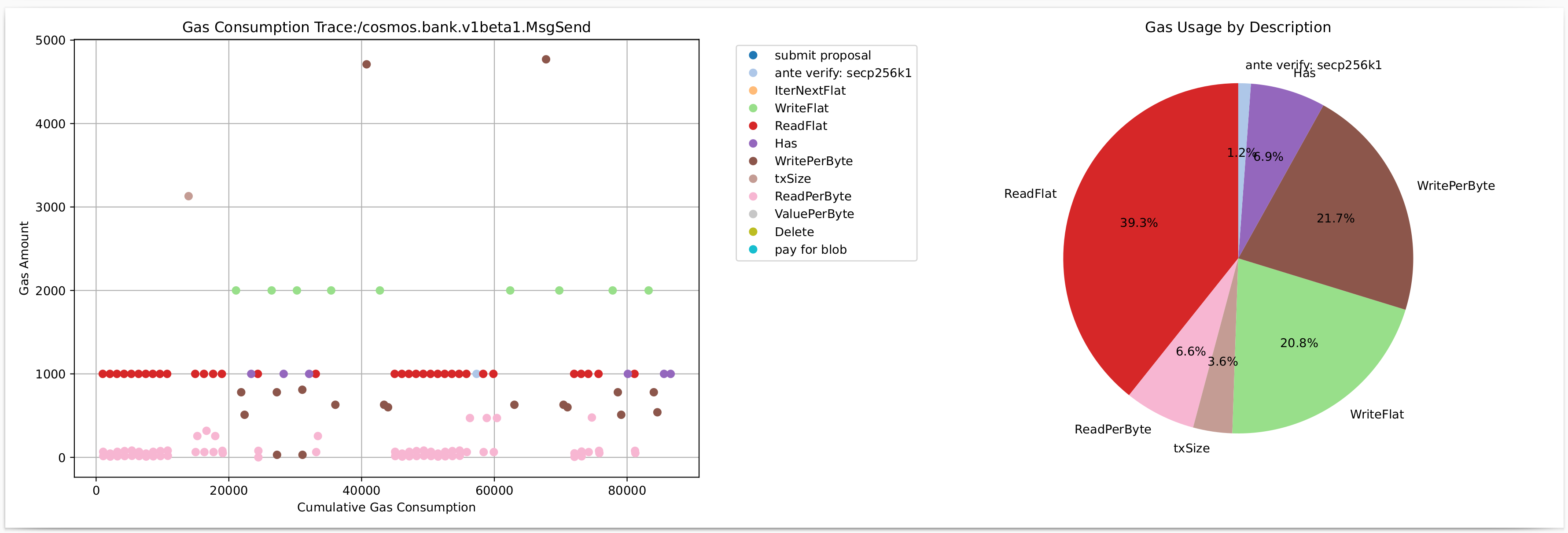
MsgCreateValidator
Here we examine a more complex transaction.
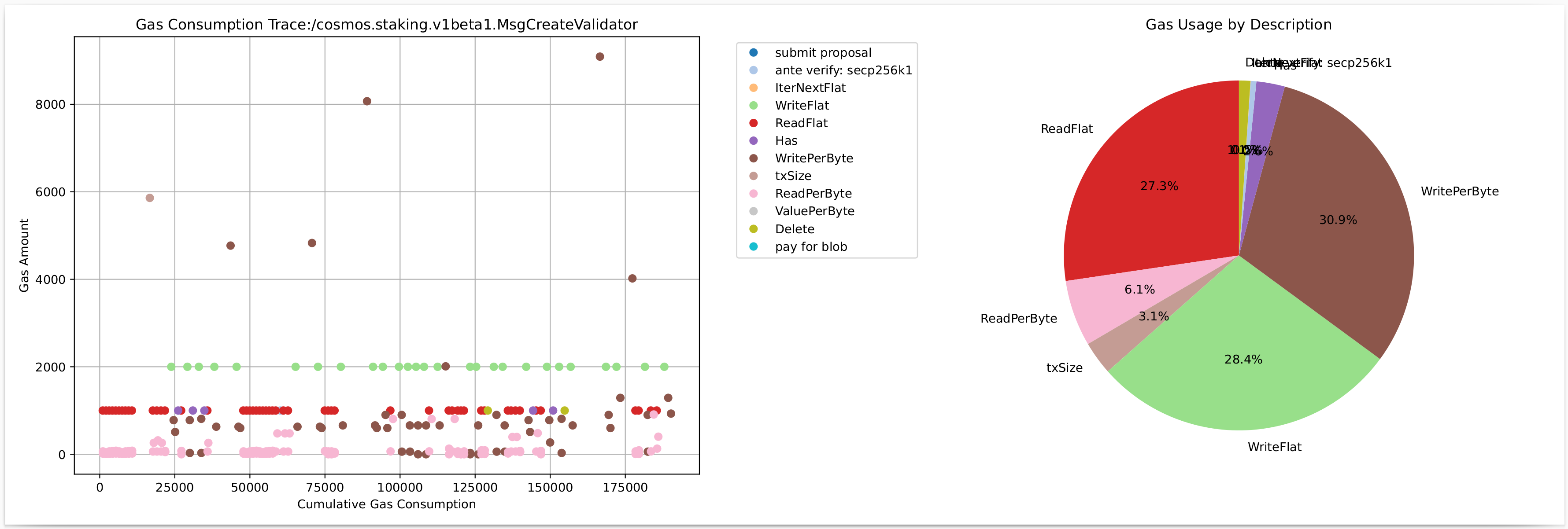
PFB with One Single Share Blob
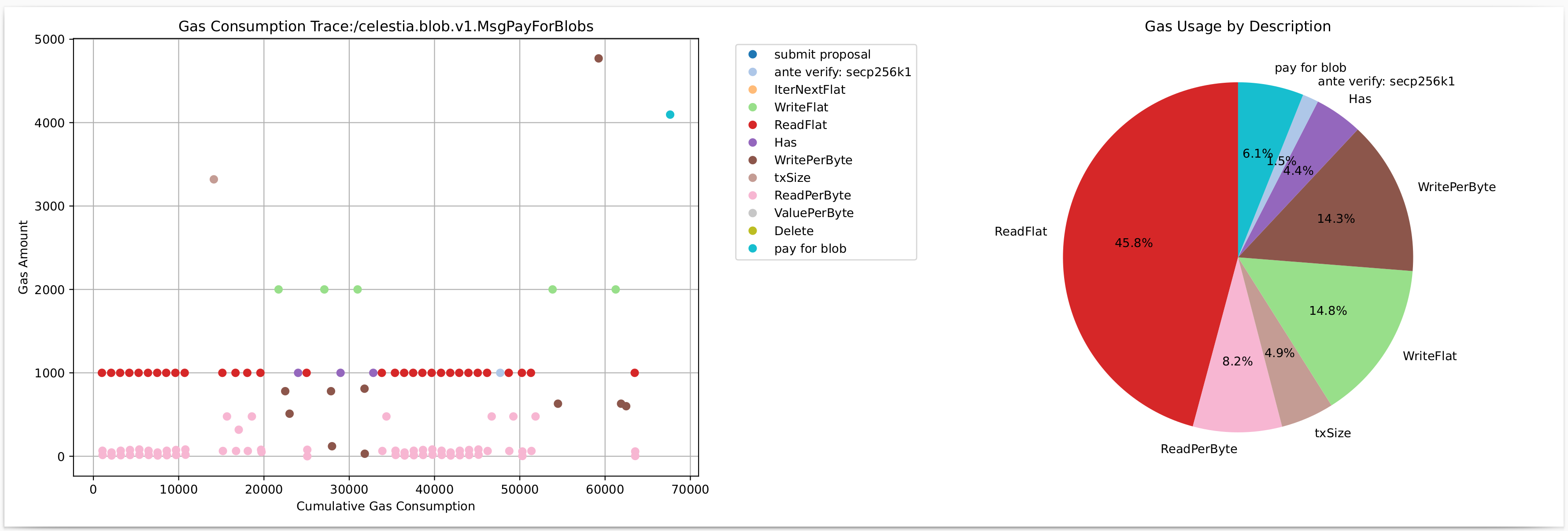
PFB with Two Single Share Blobs
This PFB transaction contains two single share blobs. Notice the gas cost for
pay for blob is double what it is above due to two shares being used, and
there is also additional cost from txSize since the transaction itself is
larger to accommodate the second set of metadata in the PFB.
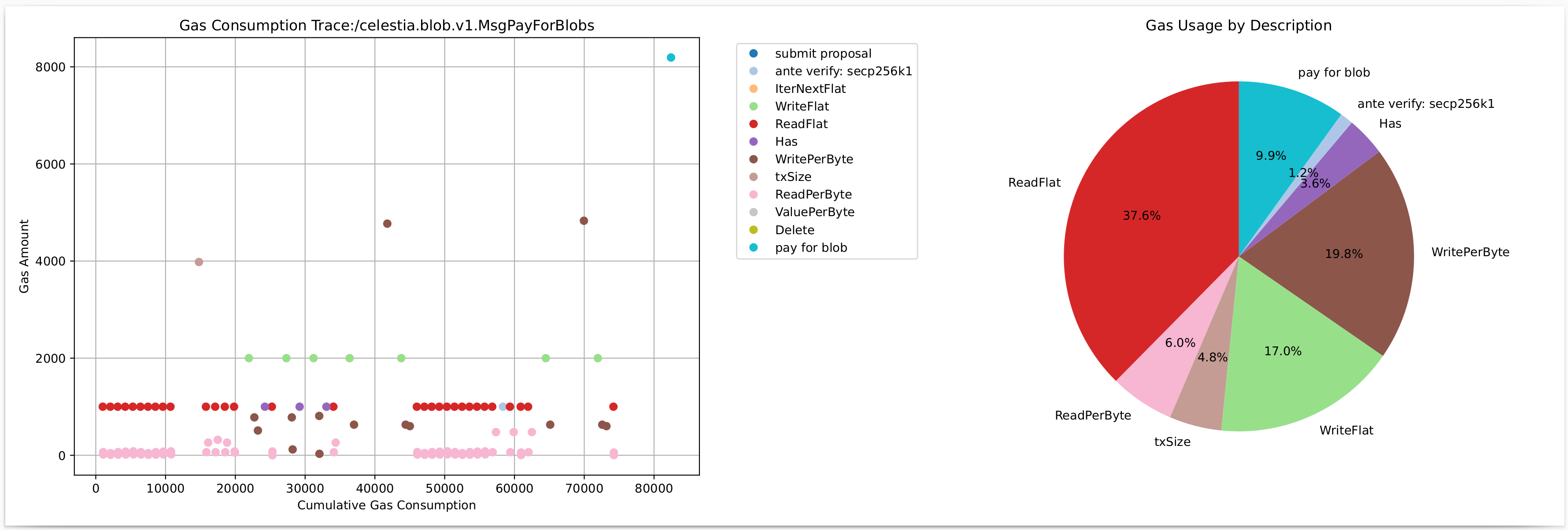
100KiB Single Blob PFB
Here we can see how the cost of a PFB with a large blob (100KiB) is quickly dominated by the cost of the blob.
Multisig
Celestia inherits support for Multisig accounts from the Cosmos SDK. Multisig accounts behave similarly to regular accounts with the added requirement that a threshold of signatures is needed to authorize a transaction.
The maximum number of signatures allowed for a multisig account is determined by the parameter auth.TxSigLimit (see parameters). The threshold and list of signers for a multisig account are set at the time of creation and can be viewed in the pubkey field of a key. For example:
$ celestia-appd keys show multisig
- address: celestia17rehcgutjfra8zhjl8675t8hhw8wsavzzutv06
name: multisig
pubkey: '{"@type":"/cosmos.crypto.multisig.LegacyAminoPubKey","threshold":2,"public_keys":[{"@type":"/cosmos.crypto.secp256k1.PubKey","key":"AxMTEFDH8oyBPIH+d2MKfCIY1yAsEd0HVekoPaAOiu9c"},{"@type":"/cosmos.crypto.secp256k1.PubKey","key":"Ax0ANkTPWcCDWy9O2TcUXw90Z0DxnX2zqPvhi4VJPUl5"},{"@type":"/cosmos.crypto.secp256k1.PubKey","key":"AlUwWCGLzhclCMEKc2YLEap9H8JT5tWq1kB8BagU1TVH"}]}'
type: multi
Please see the Cosmos SDK docs for more information on how to use multisig accounts.
State Machine Modules
Celestia app is built using the cosmos-sdk, and follows standard cosmos-sdk module structure. The modules used in the application vary based on app version:
- State Machine Modules v1
- State Machine Modules v2
- State Machine Modules v3
- State Machine Modules v4
- State Machine Modules v5
- State Machine Modules v6
- State Machine Modules v7
State Machine Modules v1
The modules used in app version 1 are:
celestia-app modules
cosmos-sdk modules
- auth
- authz
- bank
- capability
- crisis
- distribution
- evidence
- feegrant
- genutil (no spec)
- gov
- params
- slashing
- staking
- vesting (no spec)
Third-party modules
State Machine Modules v2
The modules used in app version 2 are:
celestia-app modules
cosmos-sdk modules
- auth
- authz
- bank
- capability
- crisis
- distribution
- evidence
- feegrant
- genutil (no spec)
- gov
- params
- slashing
- staking
- vesting (no spec)
Third-party modules
State Machine Modules v3
The modules used in app version 3 are:
celestia-app modules
cosmos-sdk modules
- auth
- authz
- bank
- capability
- crisis
- distribution
- evidence
- feegrant
- genutil (no spec)
- gov
- params
- slashing
- staking
- vesting (no spec)
Third-party modules
State Machine Modules v4
The modules used in app version 4 are:
celestia-app modules
cosmos-sdk modules
Third-party modules
State Machine Modules v5
The modules used in app version 5 are:
celestia-app modules
cosmos-sdk modules
Third-party modules
State Machine Modules v6
The modules used in app version 6 are:
celestia-app modules
cosmos-sdk modules
- auth
- authz
- bank
- circuit
- consensus
- distribution
- evidence
- feegrant
- genutil
- gov
- params
- slashing
- staking
- upgrade
- vesting
Third-party modules
State Machine Modules v7
The modules used in app version 7 are:
celestia-app modules
cosmos-sdk modules
- auth
- authz
- bank
- circuit
- consensus
- distribution
- evidence
- feegrant
- genutil
- gov
- params
- slashing
- staking
- upgrade
- vesting
Third-party modules
Parameters
The parameters in the application depend on the app version:
- Parameters v1
- Parameters v2
- Parameters v3
- Parameters v4
- Parameters v5
- Parameters v6
- Parameters v7
- Parameters v8
Parameters v1
The parameters below represent the parameters for app version 1.
Note that not all of these parameters are changeable via governance. This list
also includes parameters that require a hardfork to change due to being manually
hardcoded in the application or they are blocked by the x/paramfilter module.
Global parameters
| Parameter | Value | Summary | Changeable via Governance |
|---|---|---|---|
| SquareSizeUpperBound | 128 | Hardcoded maximum square size which limits the number of shares per row or column for the original data square (not yet extended). | False |
| SubtreeRootThreshold | 64 | See ADR-013 for more details. | False |
| MaxBlockSizeBytes | 100 MiB | Hardcoded value in CometBFT for the protobuf encoded block. | False |
Module parameters
| Module.Parameter | Default | Summary | Changeable via Governance |
|---|---|---|---|
| auth.MaxMemoCharacters | 256 | Largest allowed size for a memo in bytes. | True |
| auth.SigVerifyCostED25519 | 590 | Gas used to verify Ed25519 signature. | True |
| auth.SigVerifyCostSecp256k1 | 1000 | Gas used to verify secp256k1 signature. | True |
| auth.TxSigLimit | 7 | Max number of signatures allowed in a multisig transaction. | True |
| auth.TxSizeCostPerByte | 10 | Gas used per transaction byte. | True |
| bank.SendEnabled | true | Allow transfers. | False |
| blob.GasPerBlobByte | 8 | Gas used per blob byte. | True |
| blob.GovMaxSquareSize | 64 | Governance parameter for the maximum square size determined per shares per row or column for the original data square (not yet extended). If larger than MaxSquareSize, MaxSquareSize is used. | True |
| blobstream.DataCommitmentWindow | 400 | Number of blocks that are included in a signed batch (DataCommitment). | True |
| consensus.block.MaxBytes | 1974272 bytes (~1.88 MiB) | Governance parameter for the maximum size of the protobuf encoded block. | True |
| consensus.block.MaxGas | -1 | Maximum gas allowed per block (-1 is infinite). | True |
| consensus.block.TimeIotaMs | 1000 | Minimum time added to the time in the header each block. | False |
| consensus.evidence.MaxAgeDuration | 1814400000000000 (21 days) | The maximum age of evidence before it is considered invalid in nanoseconds. This value should be identical to the unbonding period. | True |
| consensus.evidence.MaxAgeNumBlocks | 120960 | The maximum number of blocks before evidence is considered invalid. This value will stop CometBFT from pruning block data. | True |
| consensus.evidence.MaxBytes | 1MiB | Maximum size in bytes used by evidence in a given block. | True |
| consensus.validator.PubKeyTypes | Ed25519 | The type of public key used by validators. | False |
| consensus.Version.AppVersion | 1 | Determines protocol rules used for a given height. Incremented by the application upon an upgrade. | True |
| distribution.BaseProposerReward | 0 | Reward in the mint denomination for proposing a block. | True |
| distribution.BonusProposerReward | 0 | Extra reward in the mint denomination for proposers based on the voting power included in the commit. | True |
| distribution.CommunityTax | 0.02 (2%) | Percentage of the inflation sent to the community pool. | True |
| distribution.WithdrawAddrEnabled | true | Enables delegators to withdraw funds to a different address. | True |
| gov.DepositParams.MaxDepositPeriod | 604800000000000 (1 week) | Maximum period for token holders to deposit on a proposal in nanoseconds. | True |
| gov.DepositParams.MinDeposit | 10_000_000_000 utia (10,000 TIA) | Minimum deposit for a proposal to enter voting period. | True |
| gov.TallyParams.Quorum | 0.334 (33.4%) | Minimum percentage of total stake needed to vote for a result to be considered valid. | True |
| gov.TallyParams.Threshold | 0.50 (50%) | Minimum proportion of Yes votes for proposal to pass. | True |
| gov.TallyParams.VetoThreshold | 0.334 (33.4%) | Minimum value of Veto votes to Total votes ratio for proposal to be vetoed. | True |
| gov.VotingParams.VotingPeriod | 604800000000000 (1 week) | Duration of the voting period in nanoseconds. | True |
| ibc.ClientGenesis.AllowedClients | []string{"06-solomachine", "07-tendermint"} | List of allowed IBC light clients. | True |
| ibc.ConnectionGenesis.MaxExpectedTimePerBlock | 7500000000000 (75 seconds) | Maximum expected time per block in nanoseconds under normal operation. | True |
| ibc.Transfer.ReceiveEnabled | true | Enable receiving tokens via IBC. | True |
| ibc.Transfer.SendEnabled | true | Enable sending tokens via IBC. | True |
| mint.BondDenom | utia | Denomination that is inflated and sent to the distribution module account. | False |
| mint.DisinflationRate | 0.10 (10%) | The rate at which the inflation rate decreases each year. | False |
| mint.InitialInflationRate | 0.08 (8%) | The inflation rate the network starts at. | False |
| mint.TargetInflationRate | 0.015 (1.5%) | The inflation rate that the network aims to stabilize at. | False |
| slashing.DowntimeJailDuration | 1 min | Duration of time a validator must stay jailed. | True |
| slashing.MinSignedPerWindow | 0.75 (75%) | The percentage of SignedBlocksWindow that must be signed not to get jailed. | True |
| slashing.SignedBlocksWindow | 5000 | The range of blocks used to count for downtime. | True |
| slashing.SlashFractionDoubleSign | 0.02 (2%) | Percentage slashed after a validator is jailed for double signing. | True |
| slashing.SlashFractionDowntime | 0.00 (0%) | Percentage slashed after a validator is jailed for downtime. | True |
| staking.BondDenom | utia | Bondable coin denomination. | False |
| staking.HistoricalEntries | 10000 | Number of historical entries to persist in store. | True |
| staking.MaxEntries | 7 | Maximum number of entries in the redelegation queue. | True |
| staking.MaxValidators | 100 | Maximum number of validators. | True |
| staking.MinCommissionRate | 0.05 (5%) | Minimum commission rate used by all validators. | True |
| staking.UnbondingTime | 1814400 (21 days) | Duration of time for unbonding in seconds. | False |
Note: none of the mint module parameters are governance modifiable because they have been converted into hardcoded constants. See the x/mint README.md for more details.
Parameters v2
The parameters below represent the parameters for app version 2.
Note that not all of these parameters are changeable via governance. This list
also includes parameter that require a hardfork to change due to being manually
hardcoded in the application or they are blocked by the x/paramfilter module.
Global parameters
| Parameter | Value | Summary | Changeable via Governance |
|---|---|---|---|
| SquareSizeUpperBound | 128 | Hardcoded maximum square size which limits the number of shares per row or column for the original data square (not yet extended). | False |
| SubtreeRootThreshold | 64 | See ADR-013 for more details. | False |
| UpgradeHeightDelay | 50400 blocks | Height based delay after a successful MsgTryUpgrade has been submitted. | False |
| MaxBlockSizeBytes | 100 MiB | Hardcoded value in CometBFT for the protobuf encoded block. | False |
Module parameters
| Module.Parameter | Default | Summary | Changeable via Governance |
|---|---|---|---|
| auth.MaxMemoCharacters | 256 | Largest allowed size for a memo in bytes. | True |
| auth.SigVerifyCostED25519 | 590 | Gas used to verify Ed25519 signature. | True |
| auth.SigVerifyCostSecp256k1 | 1000 | Gas used to verify secp256k1 signature. | True |
| auth.TxSigLimit | 7 | Max number of signatures allowed in a multisig transaction. | True |
| auth.TxSizeCostPerByte | 10 | Gas used per transaction byte. | True |
| bank.SendEnabled | true | Allow transfers. | False |
| blob.GasPerBlobByte | 8 | Gas used per blob byte. | True |
| blob.GovMaxSquareSize | 64 | Governance parameter for the maximum square size of the original data square. | True |
| consensus.block.MaxBytes | 1974272 bytes (~1.88 MiB) | Governance parameter for the maximum size of the protobuf encoded block. | True |
| consensus.block.MaxGas | -1 | Maximum gas allowed per block (-1 is infinite). | True |
| consensus.block.TimeIotaMs | 1000 | Minimum time added to the time in the header each block. | False |
| consensus.evidence.MaxAgeDuration | 1814400000000000 (21 days) | The maximum age of evidence before it is considered invalid in nanoseconds. This value should be identical to the unbonding period. | True |
| consensus.evidence.MaxAgeNumBlocks | 120960 | The maximum number of blocks before evidence is considered invalid. This value will stop CometBFT from pruning block data. | True |
| consensus.evidence.MaxBytes | 1MiB | Maximum size in bytes used by evidence in a given block. | True |
| consensus.validator.PubKeyTypes | Ed25519 | The type of public key used by validators. | False |
| consensus.Version.AppVersion | 2 | Determines protocol rules used for a given height. Incremented by the application upon an upgrade. | True |
| distribution.BaseProposerReward | 0 | Reward in the mint denomination for proposing a block. | True |
| distribution.BonusProposerReward | 0 | Extra reward in the mint denomination for proposers based on the voting power included in the commit. | True |
| distribution.CommunityTax | 0.02 (2%) | Percentage of the inflation sent to the community pool. | True |
| distribution.WithdrawAddrEnabled | true | Enables delegators to withdraw funds to a different address. | True |
| gov.DepositParams.MaxDepositPeriod | 604800000000000 (1 week) | Maximum period for token holders to deposit on a proposal in nanoseconds. | True |
| gov.DepositParams.MinDeposit | 10_000_000_000 utia (10,000 TIA) | Minimum deposit for a proposal to enter voting period. | True |
| gov.TallyParams.Quorum | 0.334 (33.4%) | Minimum percentage of total stake needed to vote for a result to be considered valid. | True |
| gov.TallyParams.Threshold | 0.50 (50%) | Minimum proportion of Yes votes for proposal to pass. | True |
| gov.TallyParams.VetoThreshold | 0.334 (33.4%) | Minimum value of Veto votes to Total votes ratio for proposal to be vetoed. | True |
| gov.VotingParams.VotingPeriod | 604800000000000 (1 week) | Duration of the voting period in nanoseconds. | True |
| ibc.ClientGenesis.AllowedClients | []string{"06-solomachine", "07-tendermint"} | List of allowed IBC light clients. | True |
| ibc.ConnectionGenesis.MaxExpectedTimePerBlock | 7500000000000 (75 seconds) | Maximum expected time per block in nanoseconds under normal operation. | True |
| ibc.Transfer.ReceiveEnabled | true | Enable receiving tokens via IBC. | True |
| ibc.Transfer.SendEnabled | true | Enable sending tokens via IBC. | True |
| icahost.HostEnabled | True | Enables or disables the Inter-Chain Accounts host module. | True |
| icahost.AllowMessages | icaAllowMessages | Defines a list of sdk message typeURLs allowed to be executed on a host chain. | True |
| minfee.NetworkMinGasPrice | 0.000001 utia | All transactions must have a gas price greater than or equal to this value. | True |
| mint.BondDenom | utia | Denomination that is inflated and sent to the distribution module account. | False |
| mint.DisinflationRate | 0.10 (10%) | The rate at which the inflation rate decreases each year. | False |
| mint.InitialInflationRate | 0.08 (8%) | The inflation rate the network starts at. | False |
| mint.TargetInflationRate | 0.015 (1.5%) | The inflation rate that the network aims to stabilize at. | False |
| packetforwardmiddleware.FeePercentage | 0 | % of the forwarded packet amount which will be subtracted and distributed to the community pool. | True |
| slashing.DowntimeJailDuration | 1 min | Duration of time a validator must stay jailed. | True |
| slashing.MinSignedPerWindow | 0.75 (75%) | The percentage of SignedBlocksWindow that must be signed not to get jailed. | True |
| slashing.SignedBlocksWindow | 5000 | The range of blocks used to count for downtime. | True |
| slashing.SlashFractionDoubleSign | 0.02 (2%) | Percentage slashed after a validator is jailed for double signing. | True |
| slashing.SlashFractionDowntime | 0.00 (0%) | Percentage slashed after a validator is jailed for downtime. | True |
| staking.BondDenom | utia | Bondable coin denomination. | False |
| staking.HistoricalEntries | 10000 | Number of historical entries to persist in store. | True |
| staking.MaxEntries | 7 | Maximum number of entries in the redelegation queue. | True |
| staking.MaxValidators | 100 | Maximum number of validators. | True |
| staking.MinCommissionRate | 0.05 (5%) | Minimum commission rate used by all validators. | True |
| staking.UnbondingTime | 1814400 (21 days) | Duration of time for unbonding in seconds. | False |
Note: none of the mint module parameters are governance modifiable because they have been converted into hardcoded constants. See the x/mint README.md for more details.
Parameters v3
The parameters below represent the parameters for app version 3.
Note that not all of these parameters are changeable via governance. This list
also includes parameter that require a hardfork to change due to being manually
hardcoded in the application or they are blocked by the x/paramfilter module.
Global parameters
| Parameter | Value | Summary | Changeable via Governance |
|---|---|---|---|
| SquareSizeUpperBound | 128 | Hardcoded maximum square size which limits the number of shares per row or column for the original data square (not yet extended). | False |
| SubtreeRootThreshold | 64 | See ADR-013 for more details. | False |
| MaxTxSize | 2 MiB | Maximum size of a transaction in bytes. | False |
| TimeoutPropose | 3500 ms | Specifies the time that validators wait during the proposal phase of the consensus process. See CometBFT specs for more details. | False |
| TimeoutCommit | 4200 ms | Specifies the duration that validators wait during the Commit phase of the consensus process. See CometBFT specs for more details. | False |
| UpgradeHeightDelay | 100800 blocks | Height based delay after a successful MsgTryUpgrade has been submitted. | False |
| MaxBlockSizeBytes | 100 MiB | Hardcoded value in CometBFT for the protobuf encoded block. | False |
Module parameters
| Module.Parameter | Default | Summary | Changeable via Governance |
|---|---|---|---|
| auth.MaxMemoCharacters | 256 | Largest allowed size for a memo in bytes. | True |
| auth.SigVerifyCostED25519 | 590 | Gas used to verify Ed25519 signature. | True |
| auth.SigVerifyCostSecp256k1 | 1000 | Gas used to verify secp256k1 signature. | True |
| auth.TxSigLimit | 7 | Max number of signatures allowed in a multisig transaction. | True |
| auth.TxSizeCostPerByte | 10 | Gas used per transaction byte. | False |
| bank.SendEnabled | true | Allow transfers. | False |
| blob.GasPerBlobByte | 8 | Gas used per blob byte. | False |
| blob.GovMaxSquareSize | 64 | Governance parameter for the maximum square size of the original data square. | True |
| consensus.block.MaxBytes | 1974272 bytes (~1.88 MiB) | Governance parameter for the maximum size of the protobuf encoded block. | True |
| consensus.block.MaxGas | -1 | Maximum gas allowed per block (-1 is infinite). | True |
| consensus.block.TimeIotaMs | 1000 | Minimum time added to the time in the header each block. | False |
| consensus.evidence.MaxAgeDuration | 1814400000000000 (21 days) | The maximum age of evidence before it is considered invalid in nanoseconds. This value should be identical to the unbonding period. | True |
| consensus.evidence.MaxAgeNumBlocks | 120960 | The maximum number of blocks before evidence is considered invalid. This value will stop CometBFT from pruning block data. | True |
| consensus.evidence.MaxBytes | 1MiB | Maximum size in bytes used by evidence in a given block. | True |
| consensus.validator.PubKeyTypes | Ed25519 | The type of public key used by validators. | False |
| consensus.Version.AppVersion | 3 | Determines protocol rules used for a given height. Incremented by the application upon an upgrade. | True |
| distribution.BaseProposerReward | 0 | Reward in the mint denomination for proposing a block. | True |
| distribution.BonusProposerReward | 0 | Extra reward in the mint denomination for proposers based on the voting power included in the commit. | True |
| distribution.CommunityTax | 0.02 (2%) | Percentage of the inflation sent to the community pool. | True |
| distribution.WithdrawAddrEnabled | true | Enables delegators to withdraw funds to a different address. | True |
| gov.DepositParams.MaxDepositPeriod | 604800000000000 (1 week) | Maximum period for token holders to deposit on a proposal in nanoseconds. | True |
| gov.DepositParams.MinDeposit | 10_000_000_000 utia (10,000 TIA) | Minimum deposit for a proposal to enter voting period. | True |
| gov.TallyParams.Quorum | 0.334 (33.4%) | Minimum percentage of total stake needed to vote for a result to be considered valid. | True |
| gov.TallyParams.Threshold | 0.50 (50%) | Minimum proportion of Yes votes for proposal to pass. | True |
| gov.TallyParams.VetoThreshold | 0.334 (33.4%) | Minimum value of Veto votes to Total votes ratio for proposal to be vetoed. | True |
| gov.VotingParams.VotingPeriod | 604800000000000 (1 week) | Duration of the voting period in nanoseconds. | True |
| ibc.ClientGenesis.AllowedClients | []string{"06-solomachine", "07-tendermint"} | List of allowed IBC light clients. | True |
| ibc.ConnectionGenesis.MaxExpectedTimePerBlock | 7500000000000 (75 seconds) | Maximum expected time per block in nanoseconds under normal operation. | True |
| ibc.Transfer.ReceiveEnabled | true | Enable receiving tokens via IBC. | True |
| ibc.Transfer.SendEnabled | true | Enable sending tokens via IBC. | True |
| icahost.HostEnabled | True | Enables or disables the Inter-Chain Accounts host module. | True |
| icahost.AllowMessages | icaAllowMessages | Defines a list of sdk message typeURLs allowed to be executed on a host chain. | True |
| minfee.NetworkMinGasPrice | 0.000001 utia | All transactions must have a gas price greater than or equal to this value. | True |
| mint.BondDenom | utia | Denomination that is inflated and sent to the distribution module account. | False |
| mint.DisinflationRate | 0.10 (10%) | The rate at which the inflation rate decreases each year. | False |
| mint.InitialInflationRate | 0.08 (8%) | The inflation rate the network starts at. | False |
| mint.TargetInflationRate | 0.015 (1.5%) | The inflation rate that the network aims to stabilize at. | False |
| packetforwardmiddleware.FeePercentage | 0 | % of the forwarded packet amount which will be subtracted and distributed to the community pool. | True |
| slashing.DowntimeJailDuration | 1 min | Duration of time a validator must stay jailed. | True |
| slashing.MinSignedPerWindow | 0.75 (75%) | The percentage of SignedBlocksWindow that must be signed not to get jailed. | True |
| slashing.SignedBlocksWindow | 5000 | The range of blocks used to count for downtime. | True |
| slashing.SlashFractionDoubleSign | 0.02 (2%) | Percentage slashed after a validator is jailed for double signing. | True |
| slashing.SlashFractionDowntime | 0.00 (0%) | Percentage slashed after a validator is jailed for downtime. | True |
| staking.BondDenom | utia | Bondable coin denomination. | False |
| staking.HistoricalEntries | 10000 | Number of historical entries to persist in store. | True |
| staking.MaxEntries | 7 | Maximum number of entries in the redelegation queue. | True |
| staking.MaxValidators | 100 | Maximum number of validators. | True |
| staking.MinCommissionRate | 0.05 (5%) | Minimum commission rate used by all validators. | True |
| staking.UnbondingTime | 1814400 (21 days) | Duration of time for unbonding in seconds. | False |
Note: none of the mint module parameters are governance modifiable because they have been converted into hardcoded constants. See the x/mint README.md for more details.
Parameters v4
The parameters below represent the parameters for app version 4.
Note that not all of these parameters are changeable via governance. This list
also includes parameter that require a hardfork to change due to being manually
hardcoded in the application or they are blocked by the ParamFilterDecorator.
Parameters that are governance modifiables can be modified via a
MsgSubmitProposal that contains a moduleXYZ.MsgUpdateParams message.
Global parameters
| Parameter | Value | Summary | Changeable via Governance |
|---|---|---|---|
| SquareSizeUpperBound | 128 | Hardcoded maximum square size which limits the number of shares per row or column for the original data square (not yet extended). | False |
| SubtreeRootThreshold | 64 | See ADR-013 for more details. | False |
| MaxTxSize | 2 MiB | Maximum size of a transaction in bytes. | False |
| TimeoutPropose | 3500 ms | Specifies the time that validators wait during the proposal phase of the consensus process. See CometBFT specs for more details. | False |
| TimeoutCommit | 4200 ms | Specifies the duration that validators wait during the Commit phase of the consensus process. See CometBFT specs for more details. | False |
| UpgradeHeightDelay | 100800 blocks | Height based delay after a successful MsgTryUpgrade has been submitted. | False |
| MaxBlockSizeBytes | 100 MiB | Hardcoded value in CometBFT for the protobuf encoded block. | False |
Module parameters
| Module.Parameter | Default | Summary | Changeable via Governance |
|---|---|---|---|
| auth.MaxMemoCharacters | 256 | Largest allowed size for a memo in bytes. | True |
| auth.SigVerifyCostED25519 | 590 | Gas used to verify Ed25519 signature. | True |
| auth.SigVerifyCostSecp256k1 | 1000 | Gas used to verify secp256k1 signature. | True |
| auth.TxSigLimit | 7 | Max number of signatures allowed in a multisig transaction. | True |
| auth.TxSizeCostPerByte | 10 | Gas used per transaction byte. | False |
| bank.SendEnabled | true | Allow transfers. | False |
| blob.GasPerBlobByte | 8 | Gas used per blob byte. | False |
| blob.GovMaxSquareSize | 64 | Governance parameter for the maximum square size of the original data square. | True |
| consensus.block.MaxBytes | 1974272 bytes (~1.88 MiB) | Governance parameter for the maximum size of the protobuf encoded block. | True |
| consensus.block.MaxGas | -1 | Maximum gas allowed per block (-1 is infinite). | True |
| consensus.block.TimeIotaMs | 1000 | Minimum time added to the time in the header each block. | False |
| consensus.evidence.MaxAgeDuration | 1814400000000000 (21 days) | The maximum age of evidence before it is considered invalid in nanoseconds. This value should be identical to the unbonding period. | True |
| consensus.evidence.MaxAgeNumBlocks | 120960 | The maximum number of blocks before evidence is considered invalid. This value will stop CometBFT from pruning block data. | True |
| consensus.evidence.MaxBytes | 1MiB | Maximum size in bytes used by evidence in a given block. | True |
| consensus.validator.PubKeyTypes | Ed25519 | The type of public key used by validators. | False |
| consensus.Version.AppVersion | 4 | Determines protocol rules used for a given height. Incremented by the application upon an upgrade. | True |
| distribution.BaseProposerReward | 0 | Reward in the mint denomination for proposing a block. | True |
| distribution.BonusProposerReward | 0 | Extra reward in the mint denomination for proposers based on the voting power included in the commit. | True |
| distribution.CommunityTax | 0.02 (2%) | Percentage of the inflation sent to the community pool. | True |
| distribution.WithdrawAddrEnabled | true | Enables delegators to withdraw funds to a different address. | True |
| gov.MaxDepositPeriod | 604800000000000 (1 week) | Maximum period for token holders to deposit on a proposal in nanoseconds. | True |
| gov.MinDeposit | 10_000_000_000 utia (10,000 TIA) | Minimum deposit for a proposal to enter voting period. | True |
| gov.Quorum | 0.334 (33.4%) | Minimum percentage of total stake needed to vote for a result to be considered valid. | True |
| gov.Threshold | 0.50 (50%) | Minimum proportion of Yes votes for proposal to pass. | True |
| gov.VetoThreshold | 0.334 (33.4%) | Minimum value of Veto votes to Total votes ratio for proposal to be vetoed. | True |
| gov.VotingPeriod | 604800000000000 (1 week) | Duration of the voting period in nanoseconds. | True |
| gov.ExpeditedMinDeposit | 50_000_000_000 utia (50,000 TIA) | Minimum deposit for an expedited proposal. | True |
| gov.ExpeditedVotingPeriod | 86400000000000 (1 day) | Duration of the expedited voting period in nanoseconds. | True |
| gov.ExpeditedThreshold | 0.667 (66.7%) | Minimum proportion of Yes votes for an expedited proposal to pass. | True |
| ibc.ClientGenesis.AllowedClients | []string{"06-solomachine", "07-tendermint"} | List of allowed IBC light clients. | True |
| ibc.ConnectionGenesis.MaxExpectedTimePerBlock | 7500000000000 (75 seconds) | Maximum expected time per block in nanoseconds under normal operation. | True |
| ibc.Transfer.ReceiveEnabled | true | Enable receiving tokens via IBC. | True |
| ibc.Transfer.SendEnabled | true | Enable sending tokens via IBC. | True |
| icahost.HostEnabled | True | Enables or disables the Inter-Chain Accounts host module. | True |
| icahost.AllowMessages | icaAllowMessages | Defines a list of sdk message typeURLs allowed to be executed on a host chain. | True |
| minfee.NetworkMinGasPrice | 0.000001 utia | All transactions must have a gas price greater than or equal to this value. | True |
| mint.BondDenom | utia | Denomination that is inflated and sent to the distribution module account. | False |
| mint.DisinflationRate | 0.067 (6.7%) | The rate at which the inflation rate decreases each year. | False |
| mint.InitialInflationRate | 0.0536 (5.36%) | The inflation rate the network starts at. | False |
| mint.TargetInflationRate | 0.015 (1.5%) | The inflation rate that the network aims to stabilize at. | False |
| packetforwardmiddleware.FeePercentage | 0 | % of the forwarded packet amount which will be subtracted and distributed to the community pool. | True |
| slashing.DowntimeJailDuration | 1 min | Duration of time a validator must stay jailed. | True |
| slashing.MinSignedPerWindow | 0.75 (75%) | The percentage of SignedBlocksWindow that must be signed not to get jailed. | True |
| slashing.SignedBlocksWindow | 5000 | The range of blocks used to count for downtime. | True |
| slashing.SlashFractionDoubleSign | 0.02 (2%) | Percentage slashed after a validator is jailed for double signing. | True |
| slashing.SlashFractionDowntime | 0.00 (0%) | Percentage slashed after a validator is jailed for downtime. | True |
| staking.BondDenom | utia | Bondable coin denomination. | False |
| staking.HistoricalEntries | 10000 | Number of historical entries to persist in store. | True |
| staking.MaxEntries | 7 | Maximum number of entries in the redelegation queue. | True |
| staking.MaxValidators | 100 | Maximum number of validators. | True |
| staking.MinCommissionRate | 0.05 (5%) | Minimum commission rate used by all validators. | True |
| staking.MaxCommissionRate | 0.25 (25%) | Maximum commission rate that validators can set when creating or updating their commission. | False |
| staking.UnbondingTime | 1814400 (21 days) | Duration of time for unbonding in seconds. | False |
Note: none of the mint module parameters are governance modifiable because they have been converted into hardcoded constants. See the x/mint README.md for more details.
Parameters v5
The parameters below represent the parameters for app version 5.
Note that not all of these parameters are changeable via governance. This list
also includes parameter that require a hardfork to change due to being manually
hardcoded in the application or they are blocked by the ParamFilterDecorator.
Parameters that are governance modifiables can be modified via a
MsgSubmitProposal that contains a moduleXYZ.MsgUpdateParams message.
Global parameters
| Parameter | Value | Summary | Changeable via Governance |
|---|---|---|---|
| SquareSizeUpperBound | 128 | Hardcoded maximum square size which limits the number of shares per row or column for the original data square (not yet extended). | False |
| SubtreeRootThreshold | 64 | See ADR-013 for more details. | False |
| MaxTxSize | 2 MiB | Maximum size of a transaction in bytes. | False |
| TimeoutPropose | 3500 ms | Specifies the time that validators wait during the proposal phase of the consensus process. See CometBFT specs for more details. | False |
| TimeoutCommit | 4200 ms | Specifies the duration that validators wait during the Commit phase of the consensus process. See CometBFT specs for more details. | False |
| UpgradeHeightDelay | 100800 blocks | Height based delay after a successful MsgTryUpgrade has been submitted. | False |
| MaxBlockSizeBytes | 100 MiB | Hardcoded value in CometBFT for the protobuf encoded block. | False |
Module parameters
| Module.Parameter | Default | Summary | Changeable via Governance |
|---|---|---|---|
| auth.MaxMemoCharacters | 256 | Largest allowed size for a memo in bytes. | True |
| auth.SigVerifyCostED25519 | 590 | Gas used to verify Ed25519 signature. | True |
| auth.SigVerifyCostSecp256k1 | 1000 | Gas used to verify secp256k1 signature. | True |
| auth.TxSigLimit | 7 | Max number of signatures allowed in a multisig transaction. | True |
| auth.TxSizeCostPerByte | 10 | Gas used per transaction byte. | False |
| bank.SendEnabled | true | Allow transfers. | False |
| blob.GasPerBlobByte | 8 | Gas used per blob byte. | False |
| blob.GovMaxSquareSize | 256 | Governance parameter for the maximum square size of the original data square. | True |
| consensus.block.MaxBytes | 1974272 bytes (~1.88 MiB) | Governance parameter for the maximum size of the protobuf encoded block. | True |
| consensus.block.MaxGas | -1 | Maximum gas allowed per block (-1 is infinite). | True |
| consensus.block.TimeIotaMs | 1000 | Minimum time added to the time in the header each block. | False |
| consensus.evidence.MaxAgeDuration | 1814400000000000 (21 days) | The maximum age of evidence before it is considered invalid in nanoseconds. This value should be identical to the unbonding period. | True |
| consensus.evidence.MaxAgeNumBlocks | 120960 | The maximum number of blocks before evidence is considered invalid. This value will stop CometBFT from pruning block data. | True |
| consensus.evidence.MaxBytes | 1MiB | Maximum size in bytes used by evidence in a given block. | True |
| consensus.validator.PubKeyTypes | Ed25519 | The type of public key used by validators. | False |
| consensus.Version.AppVersion | 5 | Determines protocol rules used for a given height. Incremented by the application upon an upgrade. | True |
| distribution.BaseProposerReward | 0 | Reward in the mint denomination for proposing a block. | True |
| distribution.BonusProposerReward | 0 | Extra reward in the mint denomination for proposers based on the voting power included in the commit. | True |
| distribution.CommunityTax | 0.02 (2%) | Percentage of the inflation sent to the community pool. | True |
| distribution.WithdrawAddrEnabled | true | Enables delegators to withdraw funds to a different address. | True |
| gov.MaxDepositPeriod | 604800000000000 (1 week) | Maximum period for token holders to deposit on a proposal in nanoseconds. | True |
| gov.MinDeposit | 10_000_000_000 utia (10,000 TIA) | Minimum deposit for a proposal to enter voting period. | True |
| gov.Quorum | 0.334 (33.4%) | Minimum percentage of total stake needed to vote for a result to be considered valid. | True |
| gov.Threshold | 0.50 (50%) | Minimum proportion of Yes votes for proposal to pass. | True |
| gov.VetoThreshold | 0.334 (33.4%) | Minimum value of Veto votes to Total votes ratio for proposal to be vetoed. | True |
| gov.VotingPeriod | 604800000000000 (1 week) | Duration of the voting period in nanoseconds. | True |
| gov.ExpeditedMinDeposit | 50_000_000_000 utia (50,000 TIA) | Minimum deposit for an expedited proposal. | True |
| gov.ExpeditedVotingPeriod | 86400000000000 (1 day) | Duration of the expedited voting period in nanoseconds. | True |
| gov.ExpeditedThreshold | 0.667 (66.7%) | Minimum proportion of Yes votes for an expedited proposal to pass. | True |
| ibc.ClientGenesis.AllowedClients | []string{"06-solomachine", "07-tendermint"} | List of allowed IBC light clients. | True |
| ibc.ConnectionGenesis.MaxExpectedTimePerBlock | 7500000000000 (75 seconds) | Maximum expected time per block in nanoseconds under normal operation. | True |
| ibc.Transfer.ReceiveEnabled | true | Enable receiving tokens via IBC. | True |
| ibc.Transfer.SendEnabled | true | Enable sending tokens via IBC. | True |
| icahost.HostEnabled | True | Enables or disables the Inter-Chain Accounts host module. | True |
| icahost.AllowMessages | icaAllowMessages | Defines a list of sdk message typeURLs allowed to be executed on a host chain. | True |
| minfee.NetworkMinGasPrice | 0.000001 utia | All transactions must have a gas price greater than or equal to this value. | True |
| mint.BondDenom | utia | Denomination that is inflated and sent to the distribution module account. | False |
| mint.DisinflationRate | 0.067 (6.7%) | The rate at which the inflation rate decreases each year. | False |
| mint.InitialInflationRate | 0.0536 (5.36%) | The inflation rate the network starts at. | False |
| mint.TargetInflationRate | 0.015 (1.5%) | The inflation rate that the network aims to stabilize at. | False |
| packetforwardmiddleware.FeePercentage | 0 | % of the forwarded packet amount which will be subtracted and distributed to the community pool. | True |
| slashing.DowntimeJailDuration | 1 min | Duration of time a validator must stay jailed. | True |
| slashing.MinSignedPerWindow | 0.75 (75%) | The percentage of SignedBlocksWindow that must be signed not to get jailed. | True |
| slashing.SignedBlocksWindow | 5000 | The range of blocks used to count for downtime. | True |
| slashing.SlashFractionDoubleSign | 0.02 (2%) | Percentage slashed after a validator is jailed for double signing. | True |
| slashing.SlashFractionDowntime | 0.00 (0%) | Percentage slashed after a validator is jailed for downtime. | True |
| staking.BondDenom | utia | Bondable coin denomination. | False |
| staking.HistoricalEntries | 10000 | Number of historical entries to persist in store. | True |
| staking.MaxEntries | 7 | Maximum number of entries in the redelegation queue. | True |
| staking.MaxValidators | 100 | Maximum number of validators. | True |
| staking.MinCommissionRate | 0.05 (5%) | Minimum commission rate used by all validators. | True |
| staking.MaxCommissionRate | 0.25 (25%) | Maximum commission rate that validators can set when creating or updating their commission. | False |
| staking.UnbondingTime | 1814400 (21 days) | Duration of time for unbonding in seconds. | False |
Note: none of the mint module parameters are governance modifiable because they have been converted into hardcoded constants. See the x/mint README.md for more details.
Parameters v6
The parameters below represent the parameters for app version 6.
Note that not all of these parameters are changeable via governance. This list
also includes parameter that require a hardfork to change due to being manually
hardcoded in the application or they are blocked by the ParamFilterDecorator.
Parameters that are governance modifiables can be modified via a
MsgSubmitProposal that contains a moduleXYZ.MsgUpdateParams message.
Global parameters
| Parameter | Value | Summary | Changeable via Governance |
|---|---|---|---|
| SquareSizeUpperBound | 512 | Hardcoded maximum square size which limits the number of shares per row or column for the original data square (not yet extended). | False |
| SubtreeRootThreshold | 64 | See ADR-013 for more details. | False |
| MaxTxSize | 8 MiB | Maximum size of a transaction in bytes. | False |
| TimeoutPropose | 8500 ms | Specifies the time that validators wait during the proposal phase of the consensus process. See CometBFT specs for more details. | False |
| TimeoutProposeDelta | 500 ms | Increase in the proposal timeout for each additional round of consensus. | False |
| TimeoutPrevote | 3000 ms | Specifies the time that validators wait for a prevote to be received. See CometBFT specs for more details. | False |
| TimeoutPrevoteDelta | 500 ms | Increase in the prevote timeout for each additional round of consensus. | False |
| TimeoutPrecommit | 3000 ms | Specifies the time that validators wait for a precommit to be received. See CometBFT specs for more details. | False |
| TimeoutPrecommitDelta | 500 ms | Increase in the precommit timeout for each additional round of consensus. | False |
| TimeoutCommit | 1 ms | Specifies the duration that validators wait after committing a block before starting on the new height. See CometBFT specs for more details. | False |
| DelayedPrecommitTimeout | 5850 ms | Time after a delayed precommit before the node proceeds to the next step. | False |
| UpgradeHeightDelay | 100800 blocks | Height based delay after a successful MsgTryUpgrade has been submitted. | False |
| MaxBlockSizeBytes | 130857600 bytes | Hardcoded value in CometBFT for the protobuf encoded block. | False |
Module parameters
| Module.Parameter | Default | Summary | Changeable via Governance |
|---|---|---|---|
| auth.MaxMemoCharacters | 256 | Largest allowed size for a memo in bytes. | True |
| auth.SigVerifyCostED25519 | 590 | Gas used to verify Ed25519 signature. | True |
| auth.SigVerifyCostSecp256k1 | 1000 | Gas used to verify secp256k1 signature. | True |
| auth.TxSigLimit | 7 | Max number of signatures allowed in a multisig transaction. | True |
| auth.TxSizeCostPerByte | 10 | Gas used per transaction byte. | False |
| bank.SendEnabled | true | Allow transfers. | False |
| blob.GasPerBlobByte | 8 | Gas used per blob byte. | False |
| blob.GovMaxSquareSize | 256 | Governance parameter for the maximum square size of the original data square. | True |
| consensus.block.MaxBytes | 32 MiB | Governance parameter for the maximum size of the protobuf encoded block. | True |
| consensus.block.MaxGas | -1 | Maximum gas allowed per block (-1 is infinite). | True |
| consensus.block.TimeIotaMs | 1000 | Minimum time added to the time in the header each block. | False |
| consensus.evidence.MaxAgeDuration | 337 hours | The maximum age of evidence before it is considered invalid in nanoseconds. This value should be identical to the unbonding period. | True |
| consensus.evidence.MaxAgeNumBlocks | 242,640 | The maximum number of blocks before evidence is considered invalid. This value will stop CometBFT from pruning block data. | True |
| consensus.evidence.MaxBytes | 1 MiB | Maximum size in bytes used by evidence in a given block. | True |
| consensus.validator.PubKeyTypes | Ed25519 | The type of public key used by validators. | False |
| consensus.Version.AppVersion | 6 | Determines protocol rules used for a given height. Incremented by the application upon an upgrade. | True |
| distribution.BaseProposerReward | 0 | Reward in the mint denomination for proposing a block. | True |
| distribution.BonusProposerReward | 0 | Extra reward in the mint denomination for proposers based on the voting power included in the commit. | True |
| distribution.CommunityTax | 0.02 (2%) | Percentage of the inflation sent to the community pool. | True |
| distribution.WithdrawAddrEnabled | true | Enables delegators to withdraw funds to a different address. | True |
| gov.MaxDepositPeriod | 604800000000000 (1 week) | Maximum period for token holders to deposit on a proposal in nanoseconds. | True |
| gov.MinDeposit | 10_000_000_000 utia (10,000 TIA) | Minimum deposit for a proposal to enter voting period. | True |
| gov.Quorum | 0.334 (33.4%) | Minimum percentage of total stake needed to vote for a result to be considered valid. | True |
| gov.Threshold | 0.50 (50%) | Minimum proportion of Yes votes for proposal to pass. | True |
| gov.VetoThreshold | 0.334 (33.4%) | Minimum value of Veto votes to Total votes ratio for proposal to be vetoed. | True |
| gov.VotingPeriod | 604800000000000 (1 week) | Duration of the voting period in nanoseconds. | True |
| gov.ExpeditedMinDeposit | 50_000_000_000 utia (50,000 TIA) | Minimum deposit for an expedited proposal. | True |
| gov.ExpeditedVotingPeriod | 86400000000000 (1 day) | Duration of the expedited voting period in nanoseconds. | True |
| gov.ExpeditedThreshold | 0.667 (66.7%) | Minimum proportion of Yes votes for an expedited proposal to pass. | True |
| ibc.ClientGenesis.AllowedClients | []string{"06-solomachine", "07-tendermint"} | List of allowed IBC light clients. | True |
| ibc.ConnectionGenesis.MaxExpectedTimePerBlock | 7500000000000 (75 seconds) | Maximum expected time per block in nanoseconds under normal operation. | True |
| ibc.Transfer.ReceiveEnabled | true | Enable receiving tokens via IBC. | True |
| ibc.Transfer.SendEnabled | true | Enable sending tokens via IBC. | True |
| icahost.HostEnabled | True | Enables or disables the Inter-Chain Accounts host module. | True |
| icahost.AllowMessages | icaAllowMessages | Defines a list of sdk message typeURLs allowed to be executed on a host chain. | True |
| minfee.NetworkMinGasPrice | 0.000001 utia | All transactions must have a gas price greater than or equal to this value. | True |
| mint.BondDenom | utia | Denomination that is inflated and sent to the distribution module account. | False |
| mint.DisinflationRate | 0.067 (6.7%) | The rate at which the inflation rate decreases each year. | False |
| mint.InitialInflationRate | 0.0267 (2.67%) | The inflation rate the network starts at. | False |
| mint.TargetInflationRate | 0.015 (1.5%) | The inflation rate that the network aims to stabilize at. | False |
| packetforwardmiddleware.FeePercentage | 0 | % of the forwarded packet amount which will be subtracted and distributed to the community pool. | True |
| slashing.DowntimeJailDuration | 1 min | Duration of time a validator must stay jailed. | True |
| slashing.MinSignedPerWindow | 0.75 (75%) | The percentage of SignedBlocksWindow that must be signed not to get jailed. | True |
| slashing.SignedBlocksWindow | 10000 | The range of blocks used to count for downtime. | True |
| slashing.SlashFractionDoubleSign | 0.02 (2%) | Percentage slashed after a validator is jailed for double signing. | True |
| slashing.SlashFractionDowntime | 0.00 (0%) | Percentage slashed after a validator is jailed for downtime. | True |
| staking.BondDenom | utia | Bondable coin denomination. | False |
| staking.HistoricalEntries | 10000 | Number of historical entries to persist in store. | True |
| staking.MaxEntries | 7 | Maximum number of entries in the redelegation queue. | True |
| staking.MaxValidators | 100 | Maximum number of validators. | True |
| staking.MinCommissionRate | 0.10 (10%) | Minimum commission rate used by all validators. | True |
| staking.MaxCommissionRate | 0.25 (25%) | Maximum commission rate that validators can set when creating or updating their commission. | False |
| staking.UnbondingTime | 1814400 (21 days) | Duration of time for unbonding in seconds. | False |
Note: none of the mint module parameters are governance modifiable because they have been converted into hardcoded constants. See the x/mint README.md for more details.
Parameters v7
The parameters below represent the parameters for app version 7.
Note that not all of these parameters are changeable via governance. This list
also includes parameter that require a hardfork to change due to being manually
hardcoded in the application or they are blocked by the ParamFilterDecorator.
Parameters that are governance modifiables can be modified via a
MsgSubmitProposal that contains a moduleXYZ.MsgUpdateParams message.
Global parameters
| Parameter | Value | Summary | Changeable via Governance |
|---|---|---|---|
| SquareSizeUpperBound | 512 | Hardcoded maximum square size which limits the number of shares per row or column for the original data square (not yet extended). | False |
| SubtreeRootThreshold | 64 | See ADR-013 for more details. | False |
| MaxTxSize | 8 MiB | Maximum size of a transaction in bytes. | False |
| TimeoutPropose | 8500 ms | Specifies the time that validators wait during the proposal phase of the consensus process. See CometBFT specs for more details. | False |
| TimeoutProposeDelta | 500 ms | Increase in the proposal timeout for each additional round of consensus. | False |
| TimeoutPrevote | 3000 ms | Specifies the time that validators wait for a prevote to be received. See CometBFT specs for more details. | False |
| TimeoutPrevoteDelta | 500 ms | Increase in the prevote timeout for each additional round of consensus. | False |
| TimeoutPrecommit | 3000 ms | Specifies the time that validators wait for a precommit to be received. See CometBFT specs for more details. | False |
| TimeoutPrecommitDelta | 500 ms | Increase in the precommit timeout for each additional round of consensus. | False |
| TimeoutCommit | 1 ms | Specifies the duration that validators wait after committing a block before starting on the new height. See CometBFT specs for more details. | False |
| DelayedPrecommitTimeout | 5850 ms | Time after a delayed precommit before the node proceeds to the next step. | False |
| UpgradeHeightDelay | 100800 blocks | Height based delay after a successful MsgTryUpgrade has been submitted. | False |
| MaxBlockSizeBytes | 130857600 bytes | Hardcoded value in CometBFT for the protobuf encoded block. | False |
Module parameters
| Module.Parameter | Default | Summary | Changeable via Governance |
|---|---|---|---|
| auth.MaxMemoCharacters | 256 | Largest allowed size for a memo in bytes. | True |
| auth.SigVerifyCostED25519 | 590 | Gas used to verify Ed25519 signature. | True |
| auth.SigVerifyCostSecp256k1 | 1000 | Gas used to verify secp256k1 signature. | True |
| auth.TxSigLimit | 7 | Max number of signatures allowed in a multisig transaction. | True |
| auth.TxSizeCostPerByte | 10 | Gas used per transaction byte. | False |
| bank.SendEnabled | true | Allow transfers. | False |
| blob.GasPerBlobByte | 8 | Gas used per blob byte. | False |
| blob.GovMaxSquareSize | 256 | Governance parameter for the maximum square size of the original data square. | True |
| consensus.block.MaxBytes | 32 MiB | Governance parameter for the maximum size of the protobuf encoded block. | True |
| consensus.block.MaxGas | -1 | Maximum gas allowed per block (-1 is infinite). | True |
| consensus.block.TimeIotaMs | 1000 | Minimum time added to the time in the header each block. | False |
| consensus.evidence.MaxAgeDuration | 337 hours | The maximum age of evidence before it is considered invalid in nanoseconds. This value should be identical to the unbonding period. | True |
| consensus.evidence.MaxAgeNumBlocks | 242,640 | The maximum number of blocks before evidence is considered invalid. This value will stop CometBFT from pruning block data. | True |
| consensus.evidence.MaxBytes | 1 MiB | Maximum size in bytes used by evidence in a given block. | True |
| consensus.validator.PubKeyTypes | Ed25519 | The type of public key used by validators. | False |
| consensus.Version.AppVersion | 7 | Determines protocol rules used for a given height. Incremented by the application upon an upgrade. | True |
| distribution.BaseProposerReward | 0 | Reward in the mint denomination for proposing a block. | True |
| distribution.BonusProposerReward | 0 | Extra reward in the mint denomination for proposers based on the voting power included in the commit. | True |
| distribution.CommunityTax | 0.02 (2%) | Percentage of the inflation sent to the community pool. | True |
| distribution.WithdrawAddrEnabled | true | Enables delegators to withdraw funds to a different address. | True |
| gov.MaxDepositPeriod | 604800000000000 (1 week) | Maximum period for token holders to deposit on a proposal in nanoseconds. | True |
| gov.MinDeposit | 10_000_000_000 utia (10,000 TIA) | Minimum deposit for a proposal to enter voting period. | True |
| gov.Quorum | 0.334 (33.4%) | Minimum percentage of total stake needed to vote for a result to be considered valid. | True |
| gov.Threshold | 0.50 (50%) | Minimum proportion of Yes votes for proposal to pass. | True |
| gov.VetoThreshold | 0.334 (33.4%) | Minimum value of Veto votes to Total votes ratio for proposal to be vetoed. | True |
| gov.VotingPeriod | 604800000000000 (1 week) | Duration of the voting period in nanoseconds. | True |
| gov.ExpeditedMinDeposit | 50_000_000_000 utia (50,000 TIA) | Minimum deposit for an expedited proposal. | True |
| gov.ExpeditedVotingPeriod | 86400000000000 (1 day) | Duration of the expedited voting period in nanoseconds. | True |
| gov.ExpeditedThreshold | 0.667 (66.7%) | Minimum proportion of Yes votes for an expedited proposal to pass. | True |
| ibc.ClientGenesis.AllowedClients | []string{"06-solomachine", "07-tendermint"} | List of allowed IBC light clients. | True |
| ibc.ConnectionGenesis.MaxExpectedTimePerBlock | 7500000000000 (75 seconds) | Maximum expected time per block in nanoseconds under normal operation. | True |
| ibc.Transfer.ReceiveEnabled | true | Enable receiving tokens via IBC. | True |
| ibc.Transfer.SendEnabled | true | Enable sending tokens via IBC. | True |
| icahost.HostEnabled | True | Enables or disables the Inter-Chain Accounts host module. | True |
| icahost.AllowMessages | icaAllowMessages | Defines a list of sdk message typeURLs allowed to be executed on a host chain. | True |
| minfee.NetworkMinGasPrice | 0.000001 utia | All transactions must have a gas price greater than or equal to this value. | True |
| mint.BondDenom | utia | Denomination that is inflated and sent to the distribution module account. | False |
| mint.DisinflationRate | 0.067 (6.7%) | The rate at which the inflation rate decreases each year. | False |
| mint.InitialInflationRate | 0.0267 (2.67%) | The inflation rate the network starts at. | False |
| mint.TargetInflationRate | 0.015 (1.5%) | The inflation rate that the network aims to stabilize at. | False |
| packetforwardmiddleware.FeePercentage | 0 | % of the forwarded packet amount which will be subtracted and distributed to the community pool. | True |
| slashing.DowntimeJailDuration | 1 min | Duration of time a validator must stay jailed. | True |
| slashing.MinSignedPerWindow | 0.75 (75%) | The percentage of SignedBlocksWindow that must be signed not to get jailed. | True |
| slashing.SignedBlocksWindow | 10000 | The range of blocks used to count for downtime. | True |
| slashing.SlashFractionDoubleSign | 0.02 (2%) | Percentage slashed after a validator is jailed for double signing. | True |
| slashing.SlashFractionDowntime | 0.00 (0%) | Percentage slashed after a validator is jailed for downtime. | True |
| staking.BondDenom | utia | Bondable coin denomination. | False |
| staking.HistoricalEntries | 10000 | Number of historical entries to persist in store. | True |
| staking.MaxEntries | 7 | Maximum number of entries in the redelegation queue. | True |
| staking.MaxValidators | 100 | Maximum number of validators. | True |
| staking.MinCommissionRate | 0.20 (20%) | Minimum commission rate used by all validators. | True |
| staking.MaxCommissionRate | 0.60 (60%) | Maximum commission rate that validators can set when creating or updating their commission. | False |
| staking.UnbondingTime | 1213200 (337 hours) | Duration of time for unbonding in seconds. | False |
Note: none of the mint module parameters are governance modifiable because they have been converted into hardcoded constants. See the x/mint README.md for more details.
Parameters v8
The parameters below represent the parameters for app version 8.
Note that not all of these parameters are changeable via governance. This list
also includes parameter that require a hardfork to change due to being manually
hardcoded in the application or they are blocked by the ParamFilterDecorator.
Parameters that are governance modifiables can be modified via a
MsgSubmitProposal that contains a moduleXYZ.MsgUpdateParams message.
Global parameters
| Parameter | Value | Summary | Changeable via Governance |
|---|---|---|---|
| SquareSizeUpperBound | 512 | Hardcoded maximum square size which limits the number of shares per row or column for the original data square (not yet extended). | False |
| SubtreeRootThreshold | 64 | See ADR-013 for more details. | False |
| MaxTxSize | 8 MiB | Maximum size of a transaction in bytes. | False |
| TimeoutPropose | 4500 ms | Specifies the time that validators wait during the proposal phase of the consensus process. See CometBFT specs for more details. | False |
| TimeoutProposeDelta | 500 ms | Increase in the proposal timeout for each additional round of consensus. | False |
| TimeoutPrevote | 3000 ms | Specifies the time that validators wait for a prevote to be received. See CometBFT specs for more details. | False |
| TimeoutPrevoteDelta | 500 ms | Increase in the prevote timeout for each additional round of consensus. | False |
| TimeoutPrecommit | 3000 ms | Specifies the time that validators wait for a precommit to be received. See CometBFT specs for more details. | False |
| TimeoutPrecommitDelta | 500 ms | Increase in the precommit timeout for each additional round of consensus. | False |
| TimeoutCommit | 1 ms | Specifies the duration that validators wait after committing a block before starting on the new height. See CometBFT specs for more details. | False |
| DelayedPrecommitTimeout | 2790 ms | Time after a delayed precommit before the node proceeds to the next step. | False |
| UpgradeHeightDelay | 100800 blocks | Height based delay after a successful MsgTryUpgrade has been submitted. | False |
| MaxBlockSizeBytes | 130857600 bytes | Hardcoded value in CometBFT for the protobuf encoded block. | False |
Module parameters
| Module.Parameter | Default | Summary | Changeable via Governance |
|---|---|---|---|
| auth.MaxMemoCharacters | 256 | Largest allowed size for a memo in bytes. | True |
| auth.SigVerifyCostED25519 | 590 | Gas used to verify Ed25519 signature. | True |
| auth.SigVerifyCostSecp256k1 | 1000 | Gas used to verify secp256k1 signature. | True |
| auth.TxSigLimit | 7 | Max number of signatures allowed in a multisig transaction. | True |
| auth.TxSizeCostPerByte | 10 | Gas used per transaction byte. | False |
| bank.SendEnabled | true | Allow transfers. | False |
| blob.GasPerBlobByte | 8 | Gas used per blob byte. | False |
| blob.GovMaxSquareSize | 256 | Governance parameter for the maximum square size of the original data square. | True |
| consensus.block.MaxBytes | 32 MiB | Governance parameter for the maximum size of the protobuf encoded block. | True |
| consensus.block.MaxGas | -1 | Maximum gas allowed per block (-1 is infinite). | True |
| consensus.block.TimeIotaMs | 1000 | Minimum time added to the time in the header each block. | False |
| consensus.evidence.MaxAgeDuration | 337 hours | The maximum age of evidence before it is considered invalid in nanoseconds. This value should be identical to the unbonding period. | True |
| consensus.evidence.MaxAgeNumBlocks | 242,640 | The maximum number of blocks before evidence is considered invalid. This value will stop CometBFT from pruning block data. | True |
| consensus.evidence.MaxBytes | 1 MiB | Maximum size in bytes used by evidence in a given block. | True |
| consensus.validator.PubKeyTypes | Ed25519 | The type of public key used by validators. | False |
| consensus.Version.AppVersion | 8 | Determines protocol rules used for a given height. Incremented by the application upon an upgrade. | True |
| distribution.BaseProposerReward | 0 | Reward in the mint denomination for proposing a block. | True |
| distribution.BonusProposerReward | 0 | Extra reward in the mint denomination for proposers based on the voting power included in the commit. | True |
| distribution.CommunityTax | 0.02 (2%) | Percentage of the inflation sent to the community pool. | True |
| distribution.WithdrawAddrEnabled | true | Enables delegators to withdraw funds to a different address. | True |
| gov.MaxDepositPeriod | 604800000000000 (1 week) | Maximum period for token holders to deposit on a proposal in nanoseconds. | True |
| gov.MinDeposit | 10_000_000_000 utia (10,000 TIA) | Minimum deposit for a proposal to enter voting period. | True |
| gov.Quorum | 0.334 (33.4%) | Minimum percentage of total stake needed to vote for a result to be considered valid. | True |
| gov.Threshold | 0.50 (50%) | Minimum proportion of Yes votes for proposal to pass. | True |
| gov.VetoThreshold | 0.334 (33.4%) | Minimum value of Veto votes to Total votes ratio for proposal to be vetoed. | True |
| gov.VotingPeriod | 604800000000000 (1 week) | Duration of the voting period in nanoseconds. | True |
| gov.ExpeditedMinDeposit | 50_000_000_000 utia (50,000 TIA) | Minimum deposit for an expedited proposal. | True |
| gov.ExpeditedVotingPeriod | 86400000000000 (1 day) | Duration of the expedited voting period in nanoseconds. | True |
| gov.ExpeditedThreshold | 0.667 (66.7%) | Minimum proportion of Yes votes for an expedited proposal to pass. | True |
| ibc.ClientGenesis.AllowedClients | []string{"06-solomachine", "07-tendermint"} | List of allowed IBC light clients. | True |
| ibc.ConnectionGenesis.MaxExpectedTimePerBlock | 15000000000 (15 seconds) | Maximum expected time per block in nanoseconds under normal operation. | True |
| ibc.Transfer.ReceiveEnabled | true | Enable receiving tokens via IBC. | True |
| ibc.Transfer.SendEnabled | true | Enable sending tokens via IBC. | True |
| icahost.HostEnabled | True | Enables or disables the Inter-Chain Accounts host module. | True |
| icahost.AllowMessages | icaAllowMessages | Defines a list of sdk message typeURLs allowed to be executed on a host chain. | True |
| minfee.NetworkMinGasPrice | 0.000001 utia | All transactions must have a gas price greater than or equal to this value. | True |
| mint.BondDenom | utia | Denomination that is inflated and sent to the distribution module account. | False |
| mint.DisinflationRate | 0.067 (6.7%) | The rate at which the inflation rate decreases each year. | False |
| mint.InitialInflationRate | 0.0267 (2.67%) | The inflation rate the network starts at. | False |
| mint.TargetInflationRate | 0.015 (1.5%) | The inflation rate that the network aims to stabilize at. | False |
| packetforwardmiddleware.FeePercentage | 0 | % of the forwarded packet amount which will be subtracted and distributed to the community pool. | True |
| slashing.DowntimeJailDuration | 1 min | Duration of time a validator must stay jailed. | True |
| slashing.MinSignedPerWindow | 0.75 (75%) | The percentage of SignedBlocksWindow that must be signed not to get jailed. | True |
| slashing.SignedBlocksWindow | 10000 | The range of blocks used to count for downtime. | True |
| slashing.SlashFractionDoubleSign | 0.02 (2%) | Percentage slashed after a validator is jailed for double signing. | True |
| slashing.SlashFractionDowntime | 0.00 (0%) | Percentage slashed after a validator is jailed for downtime. | True |
| staking.BondDenom | utia | Bondable coin denomination. | False |
| staking.HistoricalEntries | 10000 | Number of historical entries to persist in store. | True |
| staking.MaxEntries | 7 | Maximum number of entries in the redelegation queue. | True |
| staking.MaxValidators | 100 | Maximum number of validators. | True |
| staking.MinCommissionRate | 0.20 (20%) | Minimum commission rate used by all validators. | True |
| staking.MaxCommissionRate | 0.60 (60%) | Maximum commission rate that validators can set when creating or updating their commission. | False |
| staking.UnbondingTime | 1213200 (337 hours) | Duration of time for unbonding in seconds. | False |
Note: none of the mint module parameters are governance modifiable because they have been converted into hardcoded constants. See the x/mint README.md for more details.
Types
The following pages contain the types used by celestia-app. The target audience of these pages is block explorers and other tools that need an exhaustive list of supporrted Cosmos SDK Msg types and events.
Types v5
Msgs
The following is an exhaustive list of supported Cosmos SDK Msgs for app version 5.
/celestia.blob.v1.MsgPayForBlobs
/celestia.blob.v1.MsgUpdateBlobParams
/celestia.minfee.v1.MsgUpdateMinfeeParams
/celestia.signal.v1.MsgSignalVersion
/celestia.signal.v1.MsgTryUpgrade
/cosmos.auth.v1beta1.MsgUpdateParams
/cosmos.authz.v1beta1.MsgExec
/cosmos.authz.v1beta1.MsgGrant
/cosmos.authz.v1beta1.MsgPruneExpiredGrants
/cosmos.authz.v1beta1.MsgRevoke
/cosmos.bank.v1beta1.MsgMultiSend
/cosmos.bank.v1beta1.MsgSend
/cosmos.bank.v1beta1.MsgSetSendEnabled
/cosmos.bank.v1beta1.MsgUpdateParams
/cosmos.circuit.v1.MsgAuthorizeCircuitBreaker
/cosmos.circuit.v1.MsgResetCircuitBreaker
/cosmos.circuit.v1.MsgTripCircuitBreaker
/cosmos.consensus.v1.MsgUpdateParams
/cosmos.distribution.v1beta1.MsgCommunityPoolSpend
/cosmos.distribution.v1beta1.MsgDepositValidatorRewardsPool
/cosmos.distribution.v1beta1.MsgFundCommunityPool
/cosmos.distribution.v1beta1.MsgSetWithdrawAddress
/cosmos.distribution.v1beta1.MsgUpdateParams
/cosmos.distribution.v1beta1.MsgWithdrawDelegatorReward
/cosmos.distribution.v1beta1.MsgWithdrawValidatorCommission
/cosmos.evidence.v1beta1.MsgSubmitEvidence
/cosmos.feegrant.v1beta1.MsgGrantAllowance
/cosmos.feegrant.v1beta1.MsgPruneAllowances
/cosmos.feegrant.v1beta1.MsgRevokeAllowance
/cosmos.gov.v1.MsgCancelProposal
/cosmos.gov.v1.MsgDeposit
/cosmos.gov.v1.MsgExecLegacyContent
/cosmos.gov.v1.MsgSubmitProposal
/cosmos.gov.v1.MsgUpdateParams
/cosmos.gov.v1.MsgVote
/cosmos.gov.v1.MsgVoteWeighted
/cosmos.gov.v1beta1.MsgDeposit
/cosmos.gov.v1beta1.MsgSubmitProposal
/cosmos.gov.v1beta1.MsgVote
/cosmos.gov.v1beta1.MsgVoteWeighted
/cosmos.slashing.v1beta1.MsgUnjail
/cosmos.slashing.v1beta1.MsgUpdateParams
/cosmos.staking.v1beta1.MsgBeginRedelegate
/cosmos.staking.v1beta1.MsgCancelUnbondingDelegation
/cosmos.staking.v1beta1.MsgCreateValidator
/cosmos.staking.v1beta1.MsgDelegate
/cosmos.staking.v1beta1.MsgEditValidator
/cosmos.staking.v1beta1.MsgUndelegate
/cosmos.staking.v1beta1.MsgUpdateParams
/cosmos.upgrade.v1beta1.MsgCancelUpgrade
/cosmos.upgrade.v1beta1.MsgSoftwareUpgrade
/cosmos.vesting.v1beta1.MsgCreatePeriodicVestingAccount
/cosmos.vesting.v1beta1.MsgCreatePermanentLockedAccount
/cosmos.vesting.v1beta1.MsgCreateVestingAccount
/hyperlane.core.interchain_security.v1.MsgAnnounceValidator
/hyperlane.core.interchain_security.v1.MsgCreateMerkleRootMultisigIsm
/hyperlane.core.interchain_security.v1.MsgCreateMessageIdMultisigIsm
/hyperlane.core.interchain_security.v1.MsgCreateNoopIsm
/hyperlane.core.interchain_security.v1.MsgCreateRoutingIsm
/hyperlane.core.interchain_security.v1.MsgRemoveRoutingIsmDomain
/hyperlane.core.interchain_security.v1.MsgSetRoutingIsmDomain
/hyperlane.core.interchain_security.v1.MsgUpdateRoutingIsmOwner
/hyperlane.core.post_dispatch.v1.MsgClaim
/hyperlane.core.post_dispatch.v1.MsgCreateIgp
/hyperlane.core.post_dispatch.v1.MsgCreateMerkleTreeHook
/hyperlane.core.post_dispatch.v1.MsgCreateNoopHook
/hyperlane.core.post_dispatch.v1.MsgPayForGas
/hyperlane.core.post_dispatch.v1.MsgSetDestinationGasConfig
/hyperlane.core.post_dispatch.v1.MsgSetIgpOwner
/hyperlane.core.v1.MsgCreateMailbox
/hyperlane.core.v1.MsgProcessMessage
/hyperlane.core.v1.MsgSetMailbox
/hyperlane.warp.v1.MsgCreateCollateralToken
/hyperlane.warp.v1.MsgCreateSyntheticToken
/hyperlane.warp.v1.MsgEnrollRemoteRouter
/hyperlane.warp.v1.MsgRemoteTransfer
/hyperlane.warp.v1.MsgSetToken
/hyperlane.warp.v1.MsgSetTokenResponse
/hyperlane.warp.v1.MsgUnrollRemoteRouter
/ibc.applications.interchain_accounts.controller.v1.MsgRegisterInterchainAccount
/ibc.applications.interchain_accounts.controller.v1.MsgSendTx
/ibc.applications.interchain_accounts.controller.v1.MsgUpdateParams
/ibc.applications.interchain_accounts.host.v1.MsgModuleQuerySafe
/ibc.applications.interchain_accounts.host.v1.MsgUpdateParams
/ibc.applications.transfer.v1.MsgTransfer
/ibc.applications.transfer.v1.MsgUpdateParams
/ibc.core.channel.v1.MsgAcknowledgement
/ibc.core.channel.v1.MsgChannelCloseConfirm
/ibc.core.channel.v1.MsgChannelCloseInit
/ibc.core.channel.v1.MsgChannelOpenAck
/ibc.core.channel.v1.MsgChannelOpenConfirm
/ibc.core.channel.v1.MsgChannelOpenInit
/ibc.core.channel.v1.MsgChannelOpenTry
/ibc.core.channel.v1.MsgChannelUpgradeAck
/ibc.core.channel.v1.MsgChannelUpgradeCancel
/ibc.core.channel.v1.MsgChannelUpgradeConfirm
/ibc.core.channel.v1.MsgChannelUpgradeInit
/ibc.core.channel.v1.MsgChannelUpgradeOpen
/ibc.core.channel.v1.MsgChannelUpgradeTimeout
/ibc.core.channel.v1.MsgChannelUpgradeTry
/ibc.core.channel.v1.MsgPruneAcknowledgements
/ibc.core.channel.v1.MsgRecvPacket
/ibc.core.channel.v1.MsgTimeout
/ibc.core.channel.v1.MsgTimeoutOnClose
/ibc.core.channel.v1.MsgUpdateParams
/ibc.core.client.v1.MsgCreateClient
/ibc.core.client.v1.MsgIBCSoftwareUpgrade
/ibc.core.client.v1.MsgRecoverClient
/ibc.core.client.v1.MsgSubmitMisbehaviour
/ibc.core.client.v1.MsgUpdateClient
/ibc.core.client.v1.MsgUpdateParams
/ibc.core.client.v1.MsgUpgradeClient
/ibc.core.connection.v1.MsgConnectionOpenAck
/ibc.core.connection.v1.MsgConnectionOpenConfirm
/ibc.core.connection.v1.MsgConnectionOpenInit
/ibc.core.connection.v1.MsgConnectionOpenTry
/ibc.core.connection.v1.MsgUpdateParams
Events
The following is an exhaustive list of supported events for app version 5.
celestia.blob.v1.EventPayForBlobs
celestia.blob.v1.EventUpdateBlobParams
celestia.minfee.v1.EventUpdateMinfeeParams
cosmos.authz.v1beta1.EventGrant
cosmos.authz.v1beta1.EventPruneExpiredGrants
cosmos.authz.v1beta1.EventRevoke
cosmos.base.abci.v1beta1.StringEvent
cosmos.distribution.v1beta1.ValidatorSlashEvent
cosmos.distribution.v1beta1.ValidatorSlashEventRecord
cosmos.distribution.v1beta1.ValidatorSlashEvents
cosmos.group.v1.EventCreateGroup
cosmos.group.v1.EventCreateGroupPolicy
cosmos.group.v1.EventExec
cosmos.group.v1.EventLeaveGroup
cosmos.group.v1.EventProposalPruned
cosmos.group.v1.EventSubmitProposal
cosmos.group.v1.EventTallyError
cosmos.group.v1.EventUpdateGroup
cosmos.group.v1.EventUpdateGroupPolicy
cosmos.group.v1.EventVote
cosmos.group.v1.EventWithdrawProposal
cosmos.tx.v1beta1.GetTxsEventRequest
cosmos.tx.v1beta1.GetTxsEventResponse
envoy.config.core.v3.EventServiceConfig
hyperlane.core.interchain_security.v1.EventAnnounceStorageLocation
hyperlane.core.interchain_security.v1.EventCreateMerkleRootMultisigIsm
hyperlane.core.interchain_security.v1.EventCreateMessageIdMultisigIsm
hyperlane.core.interchain_security.v1.EventCreateNoopIsm
hyperlane.core.interchain_security.v1.EventCreateRoutingIsm
hyperlane.core.interchain_security.v1.EventRemoveRoutingIsmDomain
hyperlane.core.interchain_security.v1.EventSetRoutingIsm
hyperlane.core.interchain_security.v1.EventSetRoutingIsmDomain
hyperlane.core.post_dispatch.v1.EventClaimIgp
hyperlane.core.post_dispatch.v1.EventCreateIgp
hyperlane.core.post_dispatch.v1.EventCreateMerkleTreeHook
hyperlane.core.post_dispatch.v1.EventCreateNoopHook
hyperlane.core.post_dispatch.v1.EventGasPayment
hyperlane.core.post_dispatch.v1.EventInsertedIntoTree
hyperlane.core.post_dispatch.v1.EventSetDestinationGasConfig
hyperlane.core.post_dispatch.v1.EventSetIgp
hyperlane.core.v1.EventCreateMailbox
hyperlane.core.v1.EventDispatch
hyperlane.core.v1.EventProcess
hyperlane.core.v1.EventSetMailbox
hyperlane.warp.v1.EventCreateCollateralToken
hyperlane.warp.v1.EventCreateSyntheticToken
hyperlane.warp.v1.EventEnrollRemoteRouter
hyperlane.warp.v1.EventReceiveRemoteTransfer
hyperlane.warp.v1.EventSendRemoteTransfer
hyperlane.warp.v1.EventSetToken
hyperlane.warp.v1.EventUnrollRemoteRouter
Types v6
Msgs
The following is an exhaustive list of supported Cosmos SDK Msgs for app version 6.
/celestia.blob.v1.MsgPayForBlobs
/celestia.blob.v1.MsgUpdateBlobParams
/celestia.minfee.v1.MsgUpdateMinfeeParams
/celestia.signal.v1.MsgSignalVersion
/celestia.signal.v1.MsgTryUpgrade
/cosmos.auth.v1beta1.MsgUpdateParams
/cosmos.authz.v1beta1.MsgExec
/cosmos.authz.v1beta1.MsgGrant
/cosmos.authz.v1beta1.MsgPruneExpiredGrants
/cosmos.authz.v1beta1.MsgRevoke
/cosmos.bank.v1beta1.MsgMultiSend
/cosmos.bank.v1beta1.MsgSend
/cosmos.bank.v1beta1.MsgSetSendEnabled
/cosmos.bank.v1beta1.MsgUpdateParams
/cosmos.circuit.v1.MsgAuthorizeCircuitBreaker
/cosmos.circuit.v1.MsgResetCircuitBreaker
/cosmos.circuit.v1.MsgTripCircuitBreaker
/cosmos.consensus.v1.MsgUpdateParams
/cosmos.distribution.v1beta1.MsgCommunityPoolSpend
/cosmos.distribution.v1beta1.MsgDepositValidatorRewardsPool
/cosmos.distribution.v1beta1.MsgFundCommunityPool
/cosmos.distribution.v1beta1.MsgSetWithdrawAddress
/cosmos.distribution.v1beta1.MsgUpdateParams
/cosmos.distribution.v1beta1.MsgWithdrawDelegatorReward
/cosmos.distribution.v1beta1.MsgWithdrawValidatorCommission
/cosmos.evidence.v1beta1.MsgSubmitEvidence
/cosmos.feegrant.v1beta1.MsgGrantAllowance
/cosmos.feegrant.v1beta1.MsgPruneAllowances
/cosmos.feegrant.v1beta1.MsgRevokeAllowance
/cosmos.gov.v1.MsgCancelProposal
/cosmos.gov.v1.MsgDeposit
/cosmos.gov.v1.MsgExecLegacyContent
/cosmos.gov.v1.MsgSubmitProposal
/cosmos.gov.v1.MsgUpdateParams
/cosmos.gov.v1.MsgVote
/cosmos.gov.v1.MsgVoteWeighted
/cosmos.gov.v1beta1.MsgDeposit
/cosmos.gov.v1beta1.MsgSubmitProposal
/cosmos.gov.v1beta1.MsgVote
/cosmos.gov.v1beta1.MsgVoteWeighted
/cosmos.slashing.v1beta1.MsgUnjail
/cosmos.slashing.v1beta1.MsgUpdateParams
/cosmos.staking.v1beta1.MsgBeginRedelegate
/cosmos.staking.v1beta1.MsgCancelUnbondingDelegation
/cosmos.staking.v1beta1.MsgCreateValidator
/cosmos.staking.v1beta1.MsgDelegate
/cosmos.staking.v1beta1.MsgEditValidator
/cosmos.staking.v1beta1.MsgUndelegate
/cosmos.staking.v1beta1.MsgUpdateParams
/cosmos.upgrade.v1beta1.MsgCancelUpgrade
/cosmos.upgrade.v1beta1.MsgSoftwareUpgrade
/cosmos.vesting.v1beta1.MsgCreatePeriodicVestingAccount
/cosmos.vesting.v1beta1.MsgCreatePermanentLockedAccount
/cosmos.vesting.v1beta1.MsgCreateVestingAccount
/hyperlane.core.interchain_security.v1.MsgAnnounceValidator
/hyperlane.core.interchain_security.v1.MsgCreateMerkleRootMultisigIsm
/hyperlane.core.interchain_security.v1.MsgCreateMessageIdMultisigIsm
/hyperlane.core.interchain_security.v1.MsgCreateNoopIsm
/hyperlane.core.interchain_security.v1.MsgCreateRoutingIsm
/hyperlane.core.interchain_security.v1.MsgRemoveRoutingIsmDomain
/hyperlane.core.interchain_security.v1.MsgSetRoutingIsmDomain
/hyperlane.core.interchain_security.v1.MsgUpdateRoutingIsmOwner
/hyperlane.core.post_dispatch.v1.MsgClaim
/hyperlane.core.post_dispatch.v1.MsgCreateIgp
/hyperlane.core.post_dispatch.v1.MsgCreateMerkleTreeHook
/hyperlane.core.post_dispatch.v1.MsgCreateNoopHook
/hyperlane.core.post_dispatch.v1.MsgPayForGas
/hyperlane.core.post_dispatch.v1.MsgSetDestinationGasConfig
/hyperlane.core.post_dispatch.v1.MsgSetIgpOwner
/hyperlane.core.v1.MsgCreateMailbox
/hyperlane.core.v1.MsgProcessMessage
/hyperlane.core.v1.MsgSetMailbox
/hyperlane.warp.v1.MsgCreateCollateralToken
/hyperlane.warp.v1.MsgCreateSyntheticToken
/hyperlane.warp.v1.MsgEnrollRemoteRouter
/hyperlane.warp.v1.MsgRemoteTransfer
/hyperlane.warp.v1.MsgSetToken
/hyperlane.warp.v1.MsgSetTokenResponse
/hyperlane.warp.v1.MsgUnrollRemoteRouter
/ibc.applications.interchain_accounts.controller.v1.MsgRegisterInterchainAccount
/ibc.applications.interchain_accounts.controller.v1.MsgSendTx
/ibc.applications.interchain_accounts.controller.v1.MsgUpdateParams
/ibc.applications.interchain_accounts.host.v1.MsgModuleQuerySafe
/ibc.applications.interchain_accounts.host.v1.MsgUpdateParams
/ibc.applications.transfer.v1.MsgTransfer
/ibc.applications.transfer.v1.MsgUpdateParams
/ibc.core.channel.v1.MsgAcknowledgement
/ibc.core.channel.v1.MsgChannelCloseConfirm
/ibc.core.channel.v1.MsgChannelCloseInit
/ibc.core.channel.v1.MsgChannelOpenAck
/ibc.core.channel.v1.MsgChannelOpenConfirm
/ibc.core.channel.v1.MsgChannelOpenInit
/ibc.core.channel.v1.MsgChannelOpenTry
/ibc.core.channel.v1.MsgChannelUpgradeAck
/ibc.core.channel.v1.MsgChannelUpgradeCancel
/ibc.core.channel.v1.MsgChannelUpgradeConfirm
/ibc.core.channel.v1.MsgChannelUpgradeInit
/ibc.core.channel.v1.MsgChannelUpgradeOpen
/ibc.core.channel.v1.MsgChannelUpgradeTimeout
/ibc.core.channel.v1.MsgChannelUpgradeTry
/ibc.core.channel.v1.MsgPruneAcknowledgements
/ibc.core.channel.v1.MsgRecvPacket
/ibc.core.channel.v1.MsgTimeout
/ibc.core.channel.v1.MsgTimeoutOnClose
/ibc.core.channel.v1.MsgUpdateParams
/ibc.core.client.v1.MsgCreateClient
/ibc.core.client.v1.MsgIBCSoftwareUpgrade
/ibc.core.client.v1.MsgRecoverClient
/ibc.core.client.v1.MsgSubmitMisbehaviour
/ibc.core.client.v1.MsgUpdateClient
/ibc.core.client.v1.MsgUpdateParams
/ibc.core.client.v1.MsgUpgradeClient
/ibc.core.connection.v1.MsgConnectionOpenAck
/ibc.core.connection.v1.MsgConnectionOpenConfirm
/ibc.core.connection.v1.MsgConnectionOpenInit
/ibc.core.connection.v1.MsgConnectionOpenTry
/ibc.core.connection.v1.MsgUpdateParams
Events
The following is an exhaustive list of supported events for app version 6.
celestia.blob.v1.EventPayForBlobs
celestia.blob.v1.EventUpdateBlobParams
celestia.minfee.v1.EventUpdateMinfeeParams
cosmos.authz.v1beta1.EventGrant
cosmos.authz.v1beta1.EventPruneExpiredGrants
cosmos.authz.v1beta1.EventRevoke
cosmos.base.abci.v1beta1.StringEvent
cosmos.distribution.v1beta1.ValidatorSlashEvent
cosmos.distribution.v1beta1.ValidatorSlashEventRecord
cosmos.distribution.v1beta1.ValidatorSlashEvents
cosmos.group.v1.EventCreateGroup
cosmos.group.v1.EventCreateGroupPolicy
cosmos.group.v1.EventExec
cosmos.group.v1.EventLeaveGroup
cosmos.group.v1.EventProposalPruned
cosmos.group.v1.EventSubmitProposal
cosmos.group.v1.EventTallyError
cosmos.group.v1.EventUpdateGroup
cosmos.group.v1.EventUpdateGroupPolicy
cosmos.group.v1.EventVote
cosmos.group.v1.EventWithdrawProposal
cosmos.tx.v1beta1.GetTxsEventRequest
cosmos.tx.v1beta1.GetTxsEventResponse
envoy.config.core.v3.EventServiceConfig
hyperlane.core.interchain_security.v1.EventAnnounceStorageLocation
hyperlane.core.interchain_security.v1.EventCreateMerkleRootMultisigIsm
hyperlane.core.interchain_security.v1.EventCreateMessageIdMultisigIsm
hyperlane.core.interchain_security.v1.EventCreateNoopIsm
hyperlane.core.interchain_security.v1.EventCreateRoutingIsm
hyperlane.core.interchain_security.v1.EventRemoveRoutingIsmDomain
hyperlane.core.interchain_security.v1.EventSetRoutingIsm
hyperlane.core.interchain_security.v1.EventSetRoutingIsmDomain
hyperlane.core.post_dispatch.v1.EventClaimIgp
hyperlane.core.post_dispatch.v1.EventCreateIgp
hyperlane.core.post_dispatch.v1.EventCreateMerkleTreeHook
hyperlane.core.post_dispatch.v1.EventCreateNoopHook
hyperlane.core.post_dispatch.v1.EventGasPayment
hyperlane.core.post_dispatch.v1.EventInsertedIntoTree
hyperlane.core.post_dispatch.v1.EventSetDestinationGasConfig
hyperlane.core.post_dispatch.v1.EventSetIgp
hyperlane.core.v1.EventCreateMailbox
hyperlane.core.v1.EventDispatch
hyperlane.core.v1.EventProcess
hyperlane.core.v1.EventSetMailbox
hyperlane.warp.v1.EventCreateCollateralToken
hyperlane.warp.v1.EventCreateSyntheticToken
hyperlane.warp.v1.EventEnrollRemoteRouter
hyperlane.warp.v1.EventReceiveRemoteTransfer
hyperlane.warp.v1.EventSendRemoteTransfer
hyperlane.warp.v1.EventSetToken
hyperlane.warp.v1.EventUnrollRemoteRouter
Types v7
Msgs
The following is an exhaustive list of supported Cosmos SDK Msgs for app version 7.
/celestia.blob.v1.MsgPayForBlobs
/celestia.blob.v1.MsgUpdateBlobParams
/celestia.forwarding.v1.MsgForward
/celestia.minfee.v1.MsgUpdateMinfeeParams
/celestia.signal.v1.MsgSignalVersion
/celestia.signal.v1.MsgTryUpgrade
/celestia.zkism.v1.MsgCreateInterchainSecurityModule
/celestia.zkism.v1.MsgSubmitMessages
/celestia.zkism.v1.MsgUpdateInterchainSecurityModule
/cosmos.auth.v1beta1.MsgUpdateParams
/cosmos.authz.v1beta1.MsgExec
/cosmos.authz.v1beta1.MsgGrant
/cosmos.authz.v1beta1.MsgPruneExpiredGrants
/cosmos.authz.v1beta1.MsgRevoke
/cosmos.bank.v1beta1.MsgMultiSend
/cosmos.bank.v1beta1.MsgSend
/cosmos.bank.v1beta1.MsgSetSendEnabled
/cosmos.bank.v1beta1.MsgUpdateParams
/cosmos.circuit.v1.MsgAuthorizeCircuitBreaker
/cosmos.circuit.v1.MsgResetCircuitBreaker
/cosmos.circuit.v1.MsgTripCircuitBreaker
/cosmos.consensus.v1.MsgUpdateParams
/cosmos.distribution.v1beta1.MsgCommunityPoolSpend
/cosmos.distribution.v1beta1.MsgDepositValidatorRewardsPool
/cosmos.distribution.v1beta1.MsgFundCommunityPool
/cosmos.distribution.v1beta1.MsgSetWithdrawAddress
/cosmos.distribution.v1beta1.MsgUpdateParams
/cosmos.distribution.v1beta1.MsgWithdrawDelegatorReward
/cosmos.distribution.v1beta1.MsgWithdrawValidatorCommission
/cosmos.evidence.v1beta1.MsgSubmitEvidence
/cosmos.feegrant.v1beta1.MsgGrantAllowance
/cosmos.feegrant.v1beta1.MsgPruneAllowances
/cosmos.feegrant.v1beta1.MsgRevokeAllowance
/cosmos.gov.v1.MsgCancelProposal
/cosmos.gov.v1.MsgDeposit
/cosmos.gov.v1.MsgExecLegacyContent
/cosmos.gov.v1.MsgSubmitProposal
/cosmos.gov.v1.MsgUpdateParams
/cosmos.gov.v1.MsgVote
/cosmos.gov.v1.MsgVoteWeighted
/cosmos.gov.v1beta1.MsgDeposit
/cosmos.gov.v1beta1.MsgSubmitProposal
/cosmos.gov.v1beta1.MsgVote
/cosmos.gov.v1beta1.MsgVoteWeighted
/cosmos.slashing.v1beta1.MsgUnjail
/cosmos.slashing.v1beta1.MsgUpdateParams
/cosmos.staking.v1beta1.MsgBeginRedelegate
/cosmos.staking.v1beta1.MsgCancelUnbondingDelegation
/cosmos.staking.v1beta1.MsgCreateValidator
/cosmos.staking.v1beta1.MsgDelegate
/cosmos.staking.v1beta1.MsgEditValidator
/cosmos.staking.v1beta1.MsgUndelegate
/cosmos.staking.v1beta1.MsgUpdateParams
/cosmos.upgrade.v1beta1.MsgCancelUpgrade
/cosmos.upgrade.v1beta1.MsgSoftwareUpgrade
/cosmos.vesting.v1beta1.MsgCreatePeriodicVestingAccount
/cosmos.vesting.v1beta1.MsgCreatePermanentLockedAccount
/cosmos.vesting.v1beta1.MsgCreateVestingAccount
/hyperlane.core.interchain_security.v1.MsgAnnounceValidator
/hyperlane.core.interchain_security.v1.MsgCreateMerkleRootMultisigIsm
/hyperlane.core.interchain_security.v1.MsgCreateMessageIdMultisigIsm
/hyperlane.core.interchain_security.v1.MsgCreateNoopIsm
/hyperlane.core.interchain_security.v1.MsgCreateRoutingIsm
/hyperlane.core.interchain_security.v1.MsgRemoveRoutingIsmDomain
/hyperlane.core.interchain_security.v1.MsgSetRoutingIsmDomain
/hyperlane.core.interchain_security.v1.MsgUpdateRoutingIsmOwner
/hyperlane.core.post_dispatch.v1.MsgClaim
/hyperlane.core.post_dispatch.v1.MsgCreateIgp
/hyperlane.core.post_dispatch.v1.MsgCreateMerkleTreeHook
/hyperlane.core.post_dispatch.v1.MsgCreateNoopHook
/hyperlane.core.post_dispatch.v1.MsgPayForGas
/hyperlane.core.post_dispatch.v1.MsgSetDestinationGasConfig
/hyperlane.core.post_dispatch.v1.MsgSetIgpOwner
/hyperlane.core.v1.MsgCreateMailbox
/hyperlane.core.v1.MsgProcessMessage
/hyperlane.core.v1.MsgSetMailbox
/hyperlane.warp.v1.MsgCreateCollateralToken
/hyperlane.warp.v1.MsgCreateSyntheticToken
/hyperlane.warp.v1.MsgEnrollRemoteRouter
/hyperlane.warp.v1.MsgRemoteTransfer
/hyperlane.warp.v1.MsgSetToken
/hyperlane.warp.v1.MsgSetTokenResponse
/hyperlane.warp.v1.MsgUnrollRemoteRouter
/ibc.applications.interchain_accounts.controller.v1.MsgRegisterInterchainAccount
/ibc.applications.interchain_accounts.controller.v1.MsgSendTx
/ibc.applications.interchain_accounts.controller.v1.MsgUpdateParams
/ibc.applications.interchain_accounts.host.v1.MsgModuleQuerySafe
/ibc.applications.interchain_accounts.host.v1.MsgUpdateParams
/ibc.applications.transfer.v1.MsgTransfer
/ibc.applications.transfer.v1.MsgUpdateParams
/ibc.core.channel.v1.MsgAcknowledgement
/ibc.core.channel.v1.MsgChannelCloseConfirm
/ibc.core.channel.v1.MsgChannelCloseInit
/ibc.core.channel.v1.MsgChannelOpenAck
/ibc.core.channel.v1.MsgChannelOpenConfirm
/ibc.core.channel.v1.MsgChannelOpenInit
/ibc.core.channel.v1.MsgChannelOpenTry
/ibc.core.channel.v1.MsgChannelUpgradeAck
/ibc.core.channel.v1.MsgChannelUpgradeCancel
/ibc.core.channel.v1.MsgChannelUpgradeConfirm
/ibc.core.channel.v1.MsgChannelUpgradeInit
/ibc.core.channel.v1.MsgChannelUpgradeOpen
/ibc.core.channel.v1.MsgChannelUpgradeTimeout
/ibc.core.channel.v1.MsgChannelUpgradeTry
/ibc.core.channel.v1.MsgPruneAcknowledgements
/ibc.core.channel.v1.MsgRecvPacket
/ibc.core.channel.v1.MsgTimeout
/ibc.core.channel.v1.MsgTimeoutOnClose
/ibc.core.channel.v1.MsgUpdateParams
/ibc.core.client.v1.MsgCreateClient
/ibc.core.client.v1.MsgIBCSoftwareUpgrade
/ibc.core.client.v1.MsgRecoverClient
/ibc.core.client.v1.MsgSubmitMisbehaviour
/ibc.core.client.v1.MsgUpdateClient
/ibc.core.client.v1.MsgUpdateParams
/ibc.core.client.v1.MsgUpgradeClient
/ibc.core.connection.v1.MsgConnectionOpenAck
/ibc.core.connection.v1.MsgConnectionOpenConfirm
/ibc.core.connection.v1.MsgConnectionOpenInit
/ibc.core.connection.v1.MsgConnectionOpenTry
/ibc.core.connection.v1.MsgUpdateParams
Events
The following is an exhaustive list of supported events for app version 7.
celestia.blob.v1.EventPayForBlobs
celestia.blob.v1.EventUpdateBlobParams
celestia.forwarding.v1.EventForwardingComplete
celestia.forwarding.v1.EventTokenForwarded
celestia.minfee.v1.EventUpdateMinfeeParams
celestia.zkism.v1.EventCreateInterchainSecurityModule
celestia.zkism.v1.EventSubmitMessages
celestia.zkism.v1.EventUpdateInterchainSecurityModule
cosmos.authz.v1beta1.EventGrant
cosmos.authz.v1beta1.EventPruneExpiredGrants
cosmos.authz.v1beta1.EventRevoke
cosmos.base.abci.v1beta1.StringEvent
cosmos.distribution.v1beta1.ValidatorSlashEvent
cosmos.distribution.v1beta1.ValidatorSlashEventRecord
cosmos.distribution.v1beta1.ValidatorSlashEvents
cosmos.group.v1.EventCreateGroup
cosmos.group.v1.EventCreateGroupPolicy
cosmos.group.v1.EventExec
cosmos.group.v1.EventLeaveGroup
cosmos.group.v1.EventProposalPruned
cosmos.group.v1.EventSubmitProposal
cosmos.group.v1.EventTallyError
cosmos.group.v1.EventUpdateGroup
cosmos.group.v1.EventUpdateGroupPolicy
cosmos.group.v1.EventVote
cosmos.group.v1.EventWithdrawProposal
cosmos.tx.v1beta1.GetTxsEventRequest
cosmos.tx.v1beta1.GetTxsEventResponse
envoy.config.core.v3.EventServiceConfig
hyperlane.core.interchain_security.v1.EventAnnounceStorageLocation
hyperlane.core.interchain_security.v1.EventCreateMerkleRootMultisigIsm
hyperlane.core.interchain_security.v1.EventCreateMessageIdMultisigIsm
hyperlane.core.interchain_security.v1.EventCreateNoopIsm
hyperlane.core.interchain_security.v1.EventCreateRoutingIsm
hyperlane.core.interchain_security.v1.EventRemoveRoutingIsmDomain
hyperlane.core.interchain_security.v1.EventSetRoutingIsm
hyperlane.core.interchain_security.v1.EventSetRoutingIsmDomain
hyperlane.core.post_dispatch.v1.EventClaimIgp
hyperlane.core.post_dispatch.v1.EventCreateIgp
hyperlane.core.post_dispatch.v1.EventCreateMerkleTreeHook
hyperlane.core.post_dispatch.v1.EventCreateNoopHook
hyperlane.core.post_dispatch.v1.EventGasPayment
hyperlane.core.post_dispatch.v1.EventInsertedIntoTree
hyperlane.core.post_dispatch.v1.EventSetDestinationGasConfig
hyperlane.core.post_dispatch.v1.EventSetIgp
hyperlane.core.v1.EventCreateMailbox
hyperlane.core.v1.EventDispatch
hyperlane.core.v1.EventProcess
hyperlane.core.v1.EventSetMailbox
hyperlane.warp.v1.EventCreateCollateralToken
hyperlane.warp.v1.EventCreateSyntheticToken
hyperlane.warp.v1.EventEnrollRemoteRouter
hyperlane.warp.v1.EventReceiveRemoteTransfer
hyperlane.warp.v1.EventSendRemoteTransfer
hyperlane.warp.v1.EventSetToken
hyperlane.warp.v1.EventUnrollRemoteRouter
Transaction Client
Abstract
The Transaction Client (TxClient) provides a high-level abstraction for constructing, signing, broadcasting, and confirming transactions on Celestia chain. It handles sequence mismatches, mempool evictions, rejections and provides parallel transaction submission via worker accounts. The client is built around two reliable submission strategies: ordered (sequential) and unordered (parallel) submissions.
Protocol/Component Description
Gas Estimator
The gas estimation service is an external dependency that provides accurate gas and fee calculations for transaction submission.
Key Functionality:
TxClient calls the gas estimation service during broadcast to ensure transactions have appropriate gas limits and fees, handling sequence mismatches automatically through re-signing with corrected sequences.
Note: Gas estimation is only necessary when the user did not set gas limit and gas price in tx options.
Gas Estimator APIs:
EstimateGasPriceAndUsage(ctx context.Context, msgs []sdktypes.Msg, priority gasestimation.TxPriority, opts ...TxOption) (gasPrice float64, gasUsed uint64, err error)EstimateGasPrice(ctx context.Context, priority gasestimation.TxPriority) (float64, error)
Tx Flow
Below will be described tx flow from submission to broadcasting it on celestia chain to confirmation and how transaction client handles it. It will be split into 3 sub-sections.
Submission
Important: Currently, only the below submission patterns are reliable for submitting transactions. Other patterns like sending multiple transactions from one account without waiting for confirmation will likely cause sequence mismatches and failures.
Ordered Submission
Characteristics: Low Throughput, Sequential Submission, Less error prone
- Single Account: All transactions signed by one account
- Sequential: Max one tx per block, each tx must be confirmed before subsequent can be resubmitted
- Ordering: Transactions will likely be processed in submission order
- Low Throughput: One tx per block per account
- Use Case:
- Applications and users requiring all blobs to be signed by a single account and reliably executed.
APIs:
-
SubmitTx: Sequential submission for SDK txs (no worker queue).
-
Process: Build transaction → Broadcast → Confirm
func (client *TxClient) SubmitTx(ctx context.Context, msgs []sdktypes.Msg, opts ...TxOption) (*TxResponse, error)
-
-
SubmitPayForBlob: Sequential submission with default account (no worker queue).
-
Process: Create PFB with default account → Broadcast → Confirm
func (client *TxClient) SubmitPayForBlob(ctx context.Context, blobs []*share.Blob, opts ...TxOption) (*TxResponse, error)
-
-
SubmitPayForBlobWithAccount: Sequential submission with a specified account (bypasses worker queue).
-
Process: Create PFB with specified account → Broadcast → Confirmation
func (client *TxClient) SubmitPayForBlobWithAccount(ctx context.Context, accountName string, blobs []*share.Blob, opts ...TxOption) (*TxResponse, error)
-
Unordered Submission
Characteristics: High Throughput, Parallel submission, No Ordering
- Worker Accounts: A pool of accounts is created by the primary account, each fee-granted with unlimited allowances.
- Worker Queue: Transactions are queued and dispatched to available workers.
- Parallel Workers:
- Worker 0 = primary account
- Workers >0 = additional fee-granted accounts
- High Throughput: Multiple transactions can be submitted and processed per block concurrently, without sequence contention.
- No Ordering Guarantees: Execution order is nondeterministic; workers process transactions as they become available.
- Fee Grants: All fees are covered by the primary account, so workers operate without individual balance management.
- Account Reuse: Worker accounts are persisted across runtimes when parallel submission is enabled.
- Use Case: Best suited for applications that prioritize throughput over ordering.
Note: If initialized with only one worker, this mode behaves identically to Sequential Submission (one tx per block).
APIs:
-
SubmitPayForBlobToQueue: Uses worker queue for parallel or sequential (1 worker) submissions.
-
Process: Job queued → Worker assignment → PayForBlob creation → Broadcast → Confirmation
func (client *TxClient) SubmitPayForBlobToQueue(ctx context.Context, blobs []*share.Blob, opts ...TxOption) (*TxResponse, error)
-
-
QueueBlob: Direct job submission to worker queue.
-
Process: Job queued directly → Worker assignment → PayForBlob creation → Broadcast → Confirmation
func (client *TxClient) QueueBlob(ctx context.Context, resultC chan SubmissionResult, blobs []*share.Blob, opts ...TxOption)
-
All submission APIs ultimately delegate into the same broadcast and confirmation methods, they differ only in account selection, tx types and whether jobs go through the worker queue.
Broadcast
Broadcasting steps are universal across SDK transactions and blob transactions.
Process:
-
Build & Sign: Transaction is built and signed using the Signer
-
Gas Estimation:
- If no gas provided, simulate with minimal fee
- Call gas estimation service to determine gas usage and price
- If simulation fails due to a sequence mismatch:
- Update local sequence to expected.
- Resign and retry gas estimation.
-
Fee Setting: Fee is computed as
ceil(minGasPrice * gasLimit)unless explicitly set by the user -
Broadcast: Transaction is encoded and submitted via gRPC:
- Single-endpoint mode: Send to the default RPC endpoint.
- Multi-endpoint mode: Broadcast to all endpoints, accept the first success and cancel the rest; if all fail, return the first error.
-
Broadcast Error Handling: Common to both single and multi-endpoint modes.
- Sequence mismatch during CheckTx (mempool validation):
- Retry with corrected sequence until success or another failure.
- Update the signer’s local sequence to the expected value returned by the node.
- Reasoning: Without updating to the chain’s expected sequence, the client’s local signer falls behind and stalls. Once stalled, no new transactions can be submitted until the process is manually reset.
- Other rejections:
- Tendermint/CometBFT does not throw mempool errors for application rejections; they are set in the transaction response.
- The client must parse the response code:
-
0(
abci.CodeTypeOK) - accepted into mempool. -
Non-zero - tx was rejected; populate and return
BroadcastTxError.type BroadcastTxError struct { TxHash string // Transaction hash Code uint32 // Error code from node ErrorLog string // Detailed error message }
-
- Sequence mismatch during CheckTx (mempool validation):
-
Transaction Entry: On success, record (
signer,sequence,txBytes). -
Sequence Increment: After successful broadcast, increment the signer’s local sequence by calling signer.SetSequence()
Confirmation
After broadcast, the TxClient continuously polls the chain for transaction status until resolution. This is the tx confirmation life cycle:
-
Pending: Transaction in the mempool but not yet included, continue polling
-
Committed: Transaction included in a block.
-
If execution succeeded (response code =
abci.CodeTypeOK): return success -
If execution failed (any other response code):
- Populate
ExecutionErrorand return it to the user
type ExecutionError struct { TxHash string // Transaction hash Code uint32 // Execution result code ErrorLog string // Execution error details } - Populate
-
-
Rejected: Transaction was explicitly refused by the node during
ReCheck()(after each block commit).- Retrieve tx sequence from the tracker.
- Roll back the sequence to the retrieved tx sequence.
- Construct and return a rejection error with the tx hash and response code. (no specific error type)
-
Evicted: Transaction dropped from mempool (low fees, mempool full).
- The client resubmits using txBytes stored in the tracker.
- If resubmission fails (e.g. sequence mismatch):
- Do not resign with a new sequence. Eviction isn't final, another node might still propose this tx and resigning risks duplicate inclusion.
- Start a 1-minute eviction timeout window. If the tx is not confirmed within timeout period, construct and return an eviction error. (no specific error type)
- If resubmission is successful:
- The same tx is re-added to the node's mempool
- Continue polling until the updated status is resolved
-
Unknown/Not Found: Tx is neither evicted nor rejected or confirmed. Return error to the user that tx is unknown.
-
Once transactions are concluded (rejected/evicted/confirmed) they should get pruned from the tracker before function returns.
Message Structure/Communication Format
The client communicates with Celestia full nodes through gRPC services for transaction broadcasting, status checking, and gas estimation.
Transaction Broadcast
Request: BroadcastTxRequest { TxBytes, Mode }
Response: BroadcastTxResponse { TxHash, Code, RawLog }
Transaction Status
Request: TxStatusRequest { TxId }
Response: TxStatusResponse { Status, Height, ExecutionCode, Error }
Gas Estimation
Request: EstimateGasPriceAndUsageRequest { TxBytes, TxPriority }
Response: EstimatedGasUsed, EstimatedGasPrice
Assumptions and Considerations
-
Trusted Node: The client depends on a trusted consensus node for account state, sequence numbers, and gas estimation (no proof verification).
-
Eviction Behavior: Evictions are local to a node. A transaction evicted by one node may still be proposed by another, so users must not re-sign the transaction immediately to avoid double-spending.
-
Submission Modes: Only sequential (single account) or parallel (worker accounts with fee grants) are safe; other patterns may lead to sequence mismatches.
Implementation
TxClient implementation can be found in the celestia-app repo in the pkg/user directory
Tx Client v2 – Sequential Submission Queue
Overview
Tx Client v2 enforces per-account sequential transaction submission to prevent sequence races and minimize transaction failures.
Key properties
- Transactions are signed and broadcast strictly in sequence order
- A transaction is never re-signed, only resubmitted (which means resubmitted using the original signed bytes).
Assumptions
- The transactions conform to minimum fee requirements, so a transaction will eventually be included in a block after a bounded number of retries, given that the signer has enough funds in its account.
Error Handling
Errors are classified based on whether progress can be made without user intervention.
- Retryable: the client can resubmit the transaction.
- Terminal: the error is returned to the user and further progress requires user action.
Non-sequence errors
Errors that are not related to account sequence numbers.
Retryable
- Network errors
- Application errors like
ErrMempoolIsFull
Retryable Behavior
- Retry submission until accepted or a terminal error occurs.
Terminal
- Application errors like
ErrTxTooLarge
Terminal Behavior
- Return the error to the user immediately.
Sequence mismatch errors
Sequence mismatch errors occur when the node's expected account sequence differs from the client's sequence during submission.
Case 1: Expected sequence < client sequence
Indicates eviction or rejection of one or more previously submitted transactions that is not yet known to the client (e.g. eviction or rejection during ReCheckTx).
Case 1 Behavior
- Pause broadcasting.
- Query the status of transactions in the range
[expected_sequence, last_submitted_sequence].
For each transaction in order:
- Evicted (Retryable)
- Resubmit the transaction using the original signed bytes.
- Rejected (Terminal)
- Roll back the client sequence to the rejected transaction's sequence.
- Return the rejection error to the user.
Case 2: Expected sequence > client sequence
Indicates that the node's CheckTx state has advanced beyond the client's state.
This can happen for one of the following reasons:
- The transaction was evicted on the current node (thus not in the mempool), but was included in a block on another node.
- A different transaction with the same sequence was included in a block, implying that a transaction for the signer was submitted outside of the tx client.
Case 2 Behavior
- Pause broadcasting.
- Query the status of the transaction with the conflicting sequence.
- If the transaction is Committed:
- Treat the mismatch as Retryable.
- Advance client state accordingly.
- Resume broadcasting.
- If the transaction is not committed:
- Treat the mismatch as Terminal.
- Return an error indicating that the client state has conflicting transaction with same sequence number.
Confirmation and Monitoring
Transaction statuses are obtained via batched status queries using the tx_status_batch RPC method over a bounded set of pending transactions.
Transaction States
Pending
- No action required.
Committed
- The transaction was included in a block.
- Remove from the queue.
- Return success with execution metadata.
Committed with execution error
- The transaction was included in a block but failed during execution.
- Remove from the queue.
- Return execution error with metadata.
Evicted
- Broadcasting is paused.
- Resubmit the transaction.
- Resume broadcasting.
Rejected
- Broadcasting is paused.
- Roll back the sequence to the first rejected transaction.
- Return rejection error to the user.
Unknown
- The transaction is neither evicted, rejected, nor committed.
- Return an error indicating that the transaction status is unknown.
Implementation Notes
- Each account has a submission queue that owns transaction sequencing, signing, and submission.
- Confirmations are processed by a separate confirmation queue/worker that polls transaction statuses.
- Confirmation results are fed back to the submission queue, which remains the single point of coordination per account.
Fibre DA Specification
This is a specification of a DA protocol that extends Celestia. It uses a verifiable form of erasure coding to disseminate data such that it can be retrieved under honest majority assumptions without requiring full replication.
The specification is separated into the following sections:
- Client: Captures the user facing API, describes how rsema1d is used, how the data is diseminated, and how the user can manage their accounts and pay for fibre blobs.
- Server: Captures the API for storing user data, verifying correct construction and valid payment.
- SDK Fibre Module: Specifies how the state machine handles payment, verifyig validator signatures and deducting from the escrow account.
- Encoding: Specifies the encoding format of rows and the format of the shares in the original data square.
- SDK Registry Module: Stores a key value list of validator addresses to their respective Fibre DA provider addresses.
For specification of the rsema1d codec refer to the pkg/rsema1d README
Fibre Client
0) Glossary
- FSP: validator‑operated Fibre Service Provider.
- DFSP: preferred endpoint for non‑quorum ops (escrow queries; PFF relay).
- Commitment:
SHA256(rowRoot || rlcRoot). - PaymentPromise (PP): per
x/fibre, fields{signer, namespace, blob_size, commitment, fibre_blob_version=1, creation_timestamp:Timestamp, valset_height, signature}. - Assignment: permutation mapping
(commitment, valset@height)→ rows per validator.
1) Construction & Config
The client library can be constructed in two modes:
- Light-node backed. This mode will run a light-node in-process to fetch headers and validator sets as needed.
- Connected to a full node or a light node via RPC. This mode will query the node for headers and validator sets as needed.
// Light‑node sub-module (embedded into light client as module. Uses light nodes header module to track valsets)
NewFibdreDAModule(cfg ModuleConfig, vtMode ValTrackerMode, opts ...Option) (*Client, error)
// RPC‑backed (fetch headers/valsets via RPC)
NewFibdreDAClient(cfg ClientConfig, vtMode ValTrackerMode, opts ...Option) (*Client, error)
Key config
ChainID string(MUST be in validator sign‑bytes domain)EscrowOwner string(bech32 signer)DefaultFSPs []string(grpc endpoints)
Options
WithSendWorkers(int),WithReadWorkers(int)— concurrency controls
Sub‑components
- ValTracker — track current validator set (height, members, power).
- Keystore — PP signer key (sdk.Keyring).
- Encoder — rsema1d encode/decode, commitment, proofs.
- ShardMap — Assignment implementation.
- FSP Conns — pooled gRPC clients (Fibre, FibreAccount, PaymentProcessor).
- FibreClient: UploadRows, GetRows.
- DFSP Conn — preferred consensus endpoint(s) for
MsgPayForFibreand escrow queries.- FibrePaymentsClient: SubmitPayForFibre
- FibreAccountClient: escrow account balance, deposit, withdraw
2) Public API
// Mirror from go-square
type Namespace struct {
Version uint8 // MUST be 2
Bytes [29]byte
}
type PFFConfirmation struct {
TxHash string
Height uint64
}
type PutResult struct {
Commitment [32]byte
ValidatorSignatures [][]byte // ed25519 over preimage (see §3)
TTL *time.Time
PFFConfirmation PFFConfirmation
}
type Client interface {
// Builds PP internally, uploads, aggregates sigs, submits MsgPayForFibre.
// Errors:
//`ErrInvalidNamespace`: namespace is not version 2 or not 29 bytes.
//`ErrOversizeBlob`: data exceeds 128 MiB.
//`ErrInsufficientBalance` from FSP: not enough balance; client should not retry without increasing balance of escrow account. Response should include current balance and state proofs.
//`ErrNotEnoughSignatures`: not enough FSPs responded with valid signatures. Error will specify if power or count threshold was not met. Should include the number of valid signatures received.
//`ErrPFFSubmission`: submission of MsgPayForFibre failed (all FSPs).
//`Ctx` errors: timeouts, cancellations.
Put(ctx context.Context, ns Namespace, data []byte) (PutResult, error)
// Retrieves and reconstructs data by commitment.
// Errors:
// `ErrCommitmentNotFound`: no FSP had any rows for the commitment.
// `ErrNotEnoughRows`: not enough rows were retrieved to reconstruct the original data.
// `ErrRLCMismatch`: RLC computed from retrieved rows does not match the commitment.
// `Ctx` errors: timeouts, cancellations.
Get(ctx context.Context, ns Namespace, commitment [32]byte) ([]byte, error)
// Access to escrow account management API.
Account() AccountClient
// Closes all connections and resources.
Close() error
}
// AccountClient provides access to the DFSP's FibreAccount gRPC service.
type AccountClient interface {
// Mirrors: FibreAccount.QueryEscrowAccount
// Queries the escrow account for `signer`. Returns current & available balance.
QueryEscrowAccount(ctx context.Context, signer string) (curr_balance,avail_balance uint64, err error)
// Mirrors: FibreAccount.Deposit
// Deposits `amount` into the escrow account for `signer`. Returns new balance after deposit.
Deposit(ctx context.Context, signer string, amount sdk.Coin) (balance uint64, error)
// Mirrors: FibreAccount.Withdraw
// Requests a withdrawal of `amount` from the escrow account for `signer`.
Withdraw(ctx context.Context, signer string, amount sdk.Coin) (*PendingWithdrawal, error)
// Mirrors: FibreAccount.PendingWithdrawals
// Lists pending withdrawals for `signer`.
PendingWithdrawals(ctx context.Context, signer string) ([]PendingWithdrawal, error)
}
3) Sign‑bytes for validator signatures
Validator signatures are over the PP preimage + ChainID domain tag. APIs use google.protobuf.Timestamp for creation_timestamp.
SignBytes = SHA256(
"fibre/pp:v1" || Chain_id || signer_bytes || namespace ||
blob_size_u32be || commitment || fibre_blob_version_u32be ||
creation_timestamp_pb || valset_height_u64be
)
signer_bytes: 20‑byte account address (raw).namespace: 29 bytes (version MUST be 2).- Signature scheme: ed25519.
4) Assignment (non‑overlapping; permutation‑based)
ShardMap: Assignment(commitment, valset@height) → map[validator]rows
Inputs: seed = commitment, n = 16384, validators k = |valset@PP.creation_height|.
- Permute shares: sort
ibySHA256("share" || seed || u32be(i)). - Index validators lexicographically by
PubKey→ indicesj=0..k-1. - (OPTIONAL) Permute validators: sort
jbySHA256("validator" || seed || u32be(j)). base = n // k,r = n % k; firstrin chosen validator order getbase+1, othersbase.- Walk permuted shares handing contiguous blocks to validators in that order.
6) ValTracker
API
type ValTracker interface {
// CurrentSet returns the validator set and height at the latest known block.
CurrentSet(ctx context.Context) (vals []Validator, height int64, err error)
// Stop stops any background processes (if applicable).
Stop() error
}
type Validator struct {
Address Address // Address is hex bytes. From Tendermint heeader
PubKey crypto.PubKey
VotingPower int64
FSPAddr net.IP // FSP IP address
}
Modes
ValTrackerModeLight: use embedded light client to track headers/valsets.ValTrackerModeRPC: use json-RPC to fetch headers/valsets from remote Light or Bridge node.
5) Flows
Put()
- Validate:
0 < len(data) ≤ 128 MiB. Enforcerow_size ∈ {64B * 2^n | ≤ 32 KiB}. vals, valset_height := vt.CurrentSet(ctx).creation_timestamp := now.UTC()(Timestamp).- Encode: choose
row_size, buildrows[],proofs[],rlc_orig, computecommitment. - Construct PP:
{signer, ns(v2), blob_size, commitment, fibre_blob_version=1, creation_timestamp, valset_height}+ signer signature. - Assignment for
valset_height. - Fan‑out uploads to assigned FSPs (≤
send_workers):UploadRowsRequest{promise, commitment, rows subset + proofs, rlc_orig}→ collectvalidator_signatures. - Verify received signatures.
- Aggregate until ≥2/3 by power and by count.
- Submit
MsgPayForFibrevia DFSP; fail over to other FSPs on relay failure (best‑effort). - Return
PutResult.
Note: No proactive timeout path; normal timeout processing is handled by servers/caller.
Get()
- Get Valset:
vals, _ := vt.CurrentSet(ctx).- This could be a different validator set to the the validator set that actually has the shares. It probably won't be problematic because the validator sets will likely have a high degree of overlap and the erasure coding ensures enough redundancy
- Send
GetRowsRequest{commitment}to FSPs in parallel (≤read_workers). - Collect
GetRowsResponse{rows[], rlc_orig_coefs}from each FSP in parallel; Where rlc_orig_coefs should match only returned rows and have inclusion proofs. Verify all merkle proofs againstcommitment. - Decode data once amount of collected rows >
original_rows; cancel remaining ongoing requests. recompute & verify RLC. - Return
dataor error.
6) Account Management API (client ↔ DFSP)
The client exposes Account() which returns an AccountClient bound to the Default FSP (DFSP) and mapped 1:1 to the server's FibreAccount gRPC service. Protobuf request/response messages and on‑chain semantics are defined by the payments spec (x/fibre); the client must not diverge.
6.1 Transport & Routing
-
Endpoint: DFSP gRPC connection from client config. Best‑effort relay policy (no obligation for any given FSP to accept beyond availability).
-
Fallback: if DFSP is unavailable, client MAY connect to any other FSP from config (same API).
-
Retries: transient gRPC errors use exponential backoff with jitter.
-
Idempotency:
QueryEscrowAccount&PendingWithdrawalsare read‑only.Deposit/Withdraware not idempotent by default; callers must ensure they don't replay the same request.
6.2 Grpc Requests & Responses
Use the Protobuf messages from the payments spec:
QueryEscrowAccountRequest→QueryEscrowAccountResponseDepositRequest→DepositResponseWithdrawRequest→WithdrawResponsePendingWithdrawalsRequest→PendingWithdrawalsResponse
TODO: Consider to include optional proofs for escrow state queries so clients can verify DFSP responses (or specify an alternative proof format). If proofs are provided, define verification rules here.
6.3 Errors
TODO: Map gRPC status codes to client errors
7) Client Defaults & Metrics
send_workers = 20,read_workers = 20.- Metrics: encode latency, chosen
row_size, per‑FSP upload latency, signatures collected, quorum time, PFF submit/inclusion, balance cache age, insufficient‑proofs processed.
Fibre Server
1) Public gRPC APIs
1.1 Fibre API (data plane)
syntax = "proto3";
package fibre.v1;
import "google/protobuf/timestamp.proto";
message GF128 { bytes coeffs = 1; } // len == 16
message Commitment { bytes value = 1; } // len == 32
message RowWithProof { uint32 index = 1; bytes row = 2; bytes proof = 3; }
message RlcOrig { repeated GF128 coeffs = 1; } // len == N
// Mirrors x/fibre.PaymentPromise (names unified, Timestamp used)
message PaymentPromise {
string signer = 1; // bech32 escrow owner
bytes namespace = 2; // 29 raw bytes
uint32 blob_size = 3; // original length (pre-padding)
bytes commitment = 4; // 32 bytes
uint32 fibre_blob_version = 5; // = 1
google.protobuf.Timestamp creation_timestamp = 6; // UTC
uint64 valset_height = 7; // assignment height
bytes signature = 8; // signer signature over PP sign-bytes
}
message UploadRowsRequest {
PaymentPromise promise = 1;
Commitment commitment = 2;
repeated RowWithProof rows = 3; // this FSP's assigned subset only
RlcOrig rlc_orig = 4; // corrected field number
}
message UploadRowsResponse {
bytes validator_signature = 1; // ed25519 over SignBytes (see §2.3)
optional uint64 ttl = 2; // seconds remaining (if known)
optional uint32 backoff_ms = 10; // server hint for client backoff
}
message GetRowsRequest {
Commitment commitment = 1;
}
message GetRowsResponse {
repeated RowWithProof rows = 1; // ALL rows this FSP holds for the commitment
RlcOrig rlc_orig = 2;
optional uint64 ttl = 3;
optional uint32 backoff_ms = 10;
}
service Fibre {
rpc UploadRows(UploadRowsRequest) returns (UploadRowsResponse);
rpc GetRows(GetRowsRequest) returns (GetRowsResponse);
}
1.2 FibreAccount API (control plane)
Typed pass-through to the payments module. Message types/semantics are defined by the
x/fibrespec.
service FibreAccount {
rpc QueryEscrowAccount(QueryEscrowAccountRequest) returns (QueryEscrowAccountResponse);
rpc Deposit(DepositRequest) returns (DepositResponse);
rpc Withdraw(WithdrawRequest) returns (WithdrawResponse);
rpc PendingWithdrawals(PendingWithdrawalsRequest) returns (PendingWithdrawalsResponse);
}
1.3 PaymentProcessor API (control plane)
Server-side helpers to relay
MsgPayForFibreandMsgPaymentTimeout(best-effort).
service PaymentProcessor {
rpc SubmitPayForFibre(SubmitPFFRequest) returns (SubmitPFFResponse);
rpc SubmitPaymentTimeout(SubmitPaymentTimeoutRequest) returns (SubmitPaymentTimeoutResponse);
}
2) Handler Semantics
2.1 Fibre.UploadRows
Goal: accept rows for a specific FSP's assignment slice, verify payment authorizations and proofs, store rows with TTL, and return the validator's signature over the PP.
Flow (normative):
-
Validate stateless:
- msg size ≤ 8 MiB (enforced by max gRPC message size), TODO: update based on latest params
- size bounds:
0 < blob_size ≤ 128 MiB(derived from params), - row inclusion proof size matches
original_rowssize (network level params) signerbech32,namespaceversion=2 and 29 bytes,commitment32 bytes,fibre_blob_version == 1,creation_timestamp∈[now - withdrawal_delay - skew, now + skew],valset_height > 0,signaturepresent.
-
Proof/encoding checks:
- Verify RLC and Merkle proofs for provided
rowsagainstcommitmentandrlc_orig. - On failure:
INVALID_ARGUMENT(ErrInvalidEncoding). Note: PP remains in unprocessed; timeout may still charge.
- Verify RLC and Merkle proofs for provided
-
Idempotency checks:
- Put PP found in unprocessed index. If found already → OK (return
validator_signature)
- Put PP found in unprocessed index. If found already → OK (return
-
Stateful PP validation (payments module):
-
Call
ValidatePaymentPromise:- escrow exists,
- sufficient available balance for gas bound,
- signer signature valid,
- not processed.
-
On failure: return
FAILED_PRECONDITION(ErrInvalidPaymentPromise or ErrInsufficientBalance). With machine-readable detail code.
-
-
Assignment check:
- Load
valsetatvalset_height, runAssignment(commitment, valset). - Ensure the
rows.indexset equals the assignment slice for this FSP. - On mismatch:
PERMISSION_DENIED(ErrInvalidAssignment).
- Load
-
Persist rows (single horizon):
- Store under
(commitment, valset_height)with TTL=retention_ttl(24h), - Multiple PPs for the same commitment: store rows per PP (per
valset_height).
- Store under
-
Return validator signature:
- Sign
SignBytes(see §2.3) with validator key (ed25519), - Reply with
validator_signature, and optionalttl/backoff_ms.
- Sign
gRPC status mapping (suggested):
INVALID_ARGUMENT— malformed fields, encoding/proofs invalid.FAILED_PRECONDITION— insufficient balance, PP not valid in current window.PERMISSION_DENIED— assignment slice mismatch.ALREADY_EXISTS— if client attempts to overwrite different rows for the same (commitment, valset_height) and FSP slice.RESOURCE_EXHAUSTED— rate-limit/back-pressure (includebackoff_ms).
2.2 Fibre.GetRows
- Validate request (non-empty commitment).
- Lookup all rows this FSP holds for
commitmentacross all stored PPs. - If none:
NOT_FOUND(ErrCommitmentNotFound). - Return
rows+rlc_origandttl/backoff_mshints.
2.3 Validator SignBytes
Validators sign the PP domain to attest service for the data:
SignBytes = SHA256(
"fibre/pp:v1" || Chain_id ||
signer_bytes || namespace ||
blob_size_u32be || commitment ||
fibre_blob_version_u32be || creation_timestamp_pb || valset_height_u64be
)
signer_bytes: 20-byte raw account address.creation_timestamp_pb: protobufTimestampbytes.- Scheme: ed25519 over the above digest.
3) Internal Architecture
3.1 Components (expanded)
-
FibreServer
- Implements
Fibreservice. - Manages lifecycle, config, and subcomponents.
- Delegates to subcomponents:
StateAccessor,ValidatorTracker,ShardMap,RowsStorage,PromiseStore,RateLimiter.
- Implements
-
PromiseStore
-
Two logical indexes:
- Unprocessed: PPs seen but not finalized on-chain. Cleanup via
MsgPayForFibreorMsgPaymentTimeout.
- Unprocessed: PPs seen but not finalized on-chain. Cleanup via
-
Responsibilities:
- Idempotency checks (first-seen vs. duplicates).
- Promotes PPs from unprocessed → processed on-chain events.
- Timeouts: scans unprocessed for expirations; submits
MsgPaymentTimeout(best-effort).
-
-
RowsStorage
-
Persists
(commitment, valset_height)buckets with:- Assigned rows +
rlc_orig,
- Assigned rows +
-
TTL GC based on
retention_ttl(24h). -
Badger layout (v1):
d/<commitment>/<valset_height>→ rows blobb/<YYYYMMDDHHmm>/<commitment>/<valset_height>→ retention buckets
-
-
ValidatorTracker
- Fetches historical validator sets by height (fast-path cache + light/RPC backend).
- Exposes
Get(height) -> (valset, err)and quorum checks (power, count). - Internally listens to events from StateAccessor to keep up-to-date.
- Retains recent sets for performance (e.g., last 24h of heights). TODO: consider to lower it if memory usage is too high.
-
ShardMap
-
Deterministic assignment:
- Permutes shares by
SHA256("share"||commitment||i), - Optionally permutes validators by
SHA256("validator"||commitment||j), - Splits into contiguous ranges per validator (base/r scheme).
- Permutes shares by
-
-
StateAccessor (payments bridge)
-
Wraps queries to
x/fibre:ValidatePaymentPromise(PP),QueryEscrowAccount,PendingWithdrawals,- Relay helpers for
SubmitPayForFibre,SubmitPaymentTimeout.
-
May return proofs (if enabled) for client verification.
-
-
RateLimiter / Back-pressure
* Token buckets **per peer** and **total throughput**,
* Global concurrency caps: `max_concurrent_uploads`, `max_concurrent_gets`,
* Emits `RESOURCE_EXHAUSTED` with `backoff_ms`.
- Telemetry
* Metrics: RPS, bytes/s, assignment mismatches, proof/RLC failures, write latency, GC times, validator_sig issuance, PP validation latency, insufficient-balance events, backoff distribution.
3.2 Data Model & Keys
-
PP keys
pp/unprocessed/h/<promise_hash>→ PP metadata without user signature (signer, creation_timestamp, valset_height, gas_bound, …)pp/unprocessed/b/<YYYYMMDDHHmm>/<promise_hash>→ TTL bucket index
-
Commitment data
d/<commitment>/<valset_height>→ rows blob, rlc_origb/<YYYYMMDDHHmm>/<commitment>/<valset_height>→ TTL bucket index
Note: promise_hash = SHA256( PaymentPromise (canonical bytes) ).
3.3 Background Workers
-
BlockSubscriber
- Subscribes to app events (
EventPayForFibre, etc.), - Moves matching entries from unprocessed → processed,
- Updates local caches.
- Subscribes to app events (
-
TimeoutScanner
- Scans unprocessed for
creation_timestamp + promise_timeout ≤ now, - Submits
MsgPaymentTimeout(best-effort).
- Scans unprocessed for
-
TTLPruner
- Iterates
b/<bucket>to prune expired(commitment, valset_height)data.
- Iterates
4) Configuration
chain_id: string # domain for SignBytes
retention_ttl: 24h # single horizon
rows_per_message_limit: 166 # ≈ ceil(N / |valset|) + 1 (guard rail)
throughput_cap_bytes_per_sec: 50_485_760
payment_processing_timeout: 1h
max_concurrent_uploads: 100
max_concurrent_gets: 100
clock_skew_allowance: 5s # TODO: finalize value
TODO: rows_per_message_limit should be derived at runtime from the actual |valset| in promise.valset_height to avoid false positives.
5) Rate-Limit & DoS Controls
- Admission control: check message sizes against
rows_per_message_limitand effectiverow_size. - Per-client/total token buckets with refill tied to
throughput_cap_bytes_per_sec. - Burst caps: bound outstanding inflight bytes and RPCs per peer.
- Backoff hints: include
backoff_msin responses; prefer exponential backoff with jitter on clients. - Server enforced keepalive policy: close idle connections after a timeout (e.g., 2m).
6) Security & Correctness
- Replay protection: ChainID in SignBytes.
- Namespace enforcement: namespace version=2 only.
- Quorum thresholds: server signs upon local PP validation; on-chain acceptance still requires ≥2/3 power and ≥2/3 count (client enforces before submitting PFF).
- Clock skew: small tolerance (
clock_skew_allowance) forcreation_timestampchecks. - Multiple PPs / same commitment: store each valid PP independently (partition by
valset_height);GetRowsreturns all rows the FSP holds for the commitment.
7) Errors
| Code | When |
|---|---|
INVALID_ARGUMENT | Malformed PP fields; encoding/proof invalid; bad commitment. |
FAILED_PRECONDITION | Insufficient escrow; PP not valid in window; state mismatch. |
PERMISSION_DENIED | Assignment slice mismatch (rows not belonging to this FSP). |
NOT_FOUND | Commitment unknown to this FSP. |
ALREADY_EXISTS | Conflicting re-upload for same (commitment, valset_height). |
RESOURCE_EXHAUSTED | Rate-limit / capacity exceeded; backoff advised. |
UNAVAILABLE | Backend (node) RPC failure; try later. |
INTERNAL | Unhandled server error. |
TODO: Add machine-readable error details (e.g., {available_balance, required_payment} on balance failures).
Fibre SDK Module x/fibre
Abstract
Problem: Currently, users must wait for a MsgPayForBlob transaction to be included on-chain for a blob to be available on the network. This creates UX friction and delays data availability service.
Solution: The x/fibre module enables data availability for Fibre blobs without waiting for a transaction to be included on-chain by using a pre-funded escrow system. Users deposit funds into escrow accounts and then create signed PaymentPromises that guarantee future payment from the escrow account. This enables users to get data availability for the Fibre blob before the PaymentPromise transaction is included on-chain. This also enables validators to start providing data availability service for the Fibre blob before the PaymentPromise transaction is included on-chain.
How it works:
- A user funds their escrow account via
MsgDepositToEscrow - When a user wants to make data available, they create a PaymentPromise off-chain and submit it along with their blob data to validators.
- Validators verify the PaymentPromise off-chain and immediately start providing service for the data they received.
- Payment settlement occurs later through on-chain transactions (
MsgPayForFibre) or a timeout mechanism (MsgPaymentPromiseTimeout)
Key guarantee: A valid PaymentPromise guarantees payment for a blob, enabling validators to provide immediate service for blob data with confidence that the protocol will charge the user later when the MsgPayForFibre or MsgPaymentPromiseTimeout transactions are submitted on-chain.
Key Concepts
Fibre Blob
A Fibre blob is a piece of data that users want to make available through Celestia's data availability network with immediate service. Unlike regular blob submissions that require waiting for transaction confirmation, Fibre blobs use pre-paid escrow accounts to enable instant processing by validators.
PaymentPromise
A PaymentPromise is an off-chain signed message that commits a user to pay for a specific Fibre blob. It contains the blob commitment, size, namespace, and cryptographic proof that the user has sufficient funds in escrow. Validators can verify this promise instantly without waiting for on-chain transaction confirmation.
Escrow Account
An escrow account is a module-controlled account that holds user funds to guarantee payment for PaymentPromises. Users deposit funds in advance, and the module ensures these funds cannot be withdrawn immediately, providing validators with payment assurance so they can process Fibre blobs.
Commitment
A cryptographic hash that uniquely identifies a Fibre blob's content. Validators sign over this commitment to prove they have received and will make the data available. The commitment is eventually included in Celestia's data square.
Signature Schemes
The x/fibre module uses two different cryptographic signature schemes, following the same pattern as celestia-app:
-
User Signatures (secp256k1): PaymentPromises are signed by users using secp256k1, the same curve used for transaction submission in celestia-app.
-
Validator Signatures (ed25519): Validators sign blob commitments using ed25519, the same curve used for validator consensus signatures in celestia-app.
Contents
- Abstract
- Key Concepts
- Sequence Diagram
- State
- Messages
- Automatic State Transitions
- Events
- Queries
- Parameters
- Client
Sequence Diagrams
Fibre blob flow
sequenceDiagram
participant U as User (client)
participant V as Validator (server)
participant SM as State Machine
participant X as Anyone
Note over U,SM: 1. Setup Phase
U->>SM: MsgDepositToEscrow(amount)
SM->>SM: Create/update escrow account
Note over U,V: 2. Fibre Blob Submission
U->>U: Calculate blob commitment
U->>U: Create signed PaymentPromise
U->>V: Send blob data + PaymentPromise
Note over V,SM: 3. Validator Processing
V->>SM: ValidatePaymentPromise(payment_promise)
SM-->>V: ValidationResponse(valid, balance_ok)
alt PaymentPromise is valid
V->>V: Store blob data & start serving immediately
V->>V: Sign commitment
V-->>U: Return validator signature
else PaymentPromise is invalid
V-->>U: Reject (insufficient funds/invalid signature)
end
Note over U,SM: 4a. Happy Path - User Submits Payment
U->>U: Collect 2/3+ validator signatures
U->>SM: MsgPayForFibre(payment_promise, signatures)
SM->>SM: Verify signatures & deduct payment
SM->>SM: Include commitment in data square
Note right of SM: Commitment included in data square
Note over X,SM: 4b. Fallback - Timeout Processing
Note over X,SM: After PaymentPromiseTimeout elapses
X->>SM: MsgPaymentPromiseTimeout(payment_promise)
SM->>SM: Verify timeout & deduct payment
Note right of SM: No data square inclusion
-
Setup Phase: User deposits funds using
MsgDepositToEscrow, which creates or updates their escrow account with the specified amount. -
Fibre Blob Submission:
- User calculates the cryptographic commitment for their blob data
- User creates a signed
PaymentPromisecontaining the commitment, blob size, namespace, and escrow account reference - User sends the blob data and PaymentPromise to validators
-
Validator Processing:
- Validators query the state machine using
ValidatePaymentPromiseto validate the PaymentPromise signature, check escrow balance, and confirm the PaymentPromise hasn't been processed - If valid: validators store the blob data locally, sign the commitment, return their signature to the user, and immediately start serving the blob data
- If invalid: validators reject the request (insufficient funds, invalid signature, etc.)
- Validators query the state machine using
-
Payment Settlement (Two possible paths):
4a. Happy Path - User Submits Payment: User collects 2/3+ validator signatures and submits
MsgPayForFibre. The state machine verifies signatures, deducts payment from escrow, and includes the commitment in the data square.4b. Fallback - Timeout Processing: If the user doesn't submit
MsgPayForFibrewithin the timeout period, anyone can submitMsgPaymentPromiseTimeoutto force payment. The state machine deducts payment but does not include the commitment in the data square.
Key Insights
- Immediate Service: Validators start serving blob data as soon as they verify the PaymentPromise, before any on-chain payment
- Payment Guarantee: The PaymentPromise guarantees payment will occur either via user submission or timeout mechanism
- Data Square Inclusion: Only successful
MsgPayForFibresubmissions result in commitment inclusion in the data square
Withdrawal Processing Flow
Users can withdraw funds from their escrow accounts but withdrawals are subject to a delay period to ensure that the protocol can charge user's for any pending PaymentPromises.
sequenceDiagram
participant U as User
participant SM as State Machine
Note over U,SM: Withdrawal Request
U->>SM: MsgRequestWithdrawal(amount)
SM->>SM: Verify sufficient available_balance
SM->>SM: Decrease available_balance immediately
SM->>SM: Store withdrawal request with delay
Note right of SM: Funds locked for WithdrawalDelay period
Note over U,SM: Automatic Processing (after delay)
SM->>SM: BeginBlocker checks for available withdrawals
SM->>SM: Find withdrawals past delay period
SM->>SM: Decrease total escrow balance
SM->>U: Transfer funds to user account
SM->>SM: Remove withdrawal request
Note right of SM: Withdrawal complete
Withdrawal Flow Details
- Request Phase: User submits
MsgRequestWithdrawalspecifying the amount to withdraw - Immediate Lock: The system immediately decreases the user's
available_balanceto prevent double-spending, but keeps the funds in the escrow account - Delay Period: Funds remain locked for the
WithdrawalDelayperiod (default: 24 hours) to ensure any pending PaymentPromises can still be processed - Automatic Processing: The state machine's
BeginBlockerautomatically processes eligible withdrawals, transferring funds back to the user and updating the escrow account balance
This delay mechanism ensures that validators can trust PaymentPromises even when users have requested withdrawals, since the funds remain available for the delay period.
State
The fibre module maintains state for escrow accounts, withdrawals, and module parameters.
Escrow Accounts
Escrow accounts help guarantee payment for a signed PaymentPromise by ensuring that a user does not remove funds after validators sign over and provide service for a Fibre blob. Each address can only have one escrow account, indexed by their signer address.
// EscrowAccount helps guarantee payment for a signed PaymentPromise by ensuring
// that a user does not remove funds directly after validators sign over and
// provide service for a blob.
message EscrowAccount {
// signer is the address that controls this escrow account
string signer = 1 [(cosmos_proto.scalar) = "cosmos.AddressString"];
// balance is the total amount currently held in escrow
cosmos.base.v1beta1.Coin balance = 2 [(gogoproto.nullable) = false];
// available_balance is the amount available for new payments. This is usually
// the same as balance except if a user has requested a withdrawal in the past
// 24 hours in which case available_balance = balance - pending withdrawal
// amount.
cosmos.base.v1beta1.Coin available_balance = 3 [(gogoproto.nullable) = false];
}
Withdrawals
Withdrawal requests are tracked to implement the delay mechanism.
// Withdrawal tracks requests to withdraw funds from an escrow account. It is
// needed to implement a delay mechanism between when a withdrawal is requested
// and when it is executed. By default the withdrawal delay is 24 hours.
message Withdrawal {
// signer is the address that owns the escrow account this withdrawal is for
string signer = 1 [(cosmos_proto.scalar) = "cosmos.AddressString"];
// amount is the amount to be withdrawn
cosmos.base.v1beta1.Coin amount = 2 [(gogoproto.nullable) = false];
// requested_timestamp is the timestamp when withdrawal was requested
google.protobuf.Timestamp requested_timestamp = 3 [(gogoproto.nullable) = false, (gogoproto.stdtime) = true];
// available_timestamp is the timestamp when withdrawal becomes available for processing
// This is calculated as requested_timestamp + withdrawal_delay at creation time
google.protobuf.Timestamp available_timestamp = 4 [(gogoproto.nullable) = false, (gogoproto.stdtime) = true];
}
Processed Payments
To prevent double payment, the module tracks which payment promises have been processed. Each processed payment stores the payment promise hash and the timestamp when it was processed.
// ProcessedPayment represents a PaymentPromise that has been processed and
// stored in genesis state. ProcessedPayment intentionally omits many fields
// from the original PaymentPromise to avoid bloating the state. This exists for
// replay protection.
message ProcessedPayment {
bytes payment_promise_hash = 1;
google.protobuf.Timestamp processed_at = 2 [(gogoproto.nullable) = false, (gogoproto.stdtime) = true];
}
Processed payments use a dual-index pattern for efficient querying and pruning:
- By hash:
processed_payments_by_hash/{payment_promise_hash}→ProcessedPayment(for replay protection) - By time:
processed_payments_by_time/{processed_at}/{payment_promise_hash}→ProcessedPayment(for time-ordered pruning)
Messages
Gas Consumption
All messages use the existing gas consumption mechanism in the cosmos-sdk. In addition to the standard resource pricing, the messages that deduct fees for blobs, MsgPayForFibre and MsgPaymentPromiseTimeout, manually add gas consumption based on Fibre blob size.
Blob Gas Calculation:
Gas cost is calculated using the following formula:
total_gas = (rows * row_size(blob_size) * gas_per_blob_byte)
This means that users pay for padding as well, just like PFBs.
Where:
rowsis the constant number of rows needed for the blob datarow_size(blob_size)is the size of each row in bytesgas_per_blob_byteis the gas cost per byte parameter
MsgDepositToEscrow
Deposits funds to the signer's escrow account. If no escrow account exists for the signer, one will be created automatically. Deposits are processed instantly.
// MsgDepositToEscrow deposits funds to the signer's escrow account.
message MsgDepositToEscrow {
option (cosmos.msg.v1.signer) = "signer";
// signer is the bech32 encoded signer address
string signer = 1 [(cosmos_proto.scalar) = "cosmos.AddressString"];
// amount is the amount to deposit
cosmos.base.v1beta1.Coin amount = 2 [(gogoproto.nullable) = false];
}
Validation and Processing
Stateless Validation:
- Signer address must be valid
- Amount must be positive
Stateful Processing:
- If signer's escrow account doesn't exist, create one with zero balance
- Transfer funds from signer to module account
- Increase both balance and available_balance by deposit amount
- Emit EventDepositToEscrow
MsgRequestWithdrawal
Requests withdrawal from the signer's escrow account. Funds are withdrawn after the withdrawal delay.
// MsgRequestWithdrawal requests withdrawal from the signer's escrow account.
message MsgRequestWithdrawal {
option (cosmos.msg.v1.signer) = "signer";
// signer is the bech32 encoded signer address
string signer = 1 [(cosmos_proto.scalar) = "cosmos.AddressString"];
// amount is the amount to withdraw
cosmos.base.v1beta1.Coin amount = 2 [(gogoproto.nullable) = false];
}
Validation
Stateless Validation:
- Signer address must be valid
- Amount must be positive
Stateful Processing:
- Verify signer's escrow account exists
- Verify sufficient available balance
- Verify no existing withdrawal request at current timestamp (prevents key collision in
withdrawals_by_signer/{signer}/{requested_timestamp}index) - Calculate available_timestamp = requested_timestamp + withdrawal_delay
- Create Withdrawal with both requested_timestamp and available_timestamp
- Decrease available_balance immediately (balance remains unchanged until withdrawal is processed)
- Store withdrawal in both indexes (by signer and by available time)
- Emit EventWithdrawFromEscrowRequest
Withdrawal Processing
Withdrawals are automatically processed in BeginBlocker when current_time >= withdrawal.available_timestamp:
func processAvailableWithdrawals(ctx sdk.Context, k Keeper) {
currentTime := ctx.BlockTime()
// Iterate over withdrawals-by-available index starting from earliest timestamp
iterator := k.GetWithdrawalsByAvailableIterator(ctx, currentTime)
defer iterator.Close()
for ; iterator.Valid(); iterator.Next() {
// Parse key to extract available_at timestamp and signer address
availableAt, signer, err := k.ParseWithdrawalsByAvailableKey(iterator.Key())
if err != nil {
// Log error but continue processing other withdrawals
k.Logger(ctx).Error("failed to parse withdrawals-by-available key", "error", err)
continue
}
// Stop if we've reached withdrawals not yet available
if availableAt.After(currentTime) {
break
}
// Get full withdrawal from value
var withdrawal types.Withdrawal
k.cdc.MustUnmarshal(iterator.Value(), &withdrawal)
amount := withdrawal.Amount
// Convert signer string to AccAddress
signerAddr, err := sdk.AccAddressFromBech32(signer)
if err != nil {
// Log error but continue processing other withdrawals
k.Logger(ctx).Error("failed to parse signer address", "error", err, "signer", signer)
continue
}
// Process withdrawal: transfer from module to user account
err = k.bankKeeper.SendCoinsFromModuleToAccount(
ctx, types.ModuleName, signerAddr, sdk.NewCoins(amount))
if err != nil {
// Log error but continue processing other withdrawals
k.Logger(ctx).Error("failed to process withdrawal", "error", err, "signer", signer)
continue
}
// Update escrow account balance (decrease total balance)
escrowAccount, found := k.GetEscrowAccount(ctx, signer)
if !found {
// This shouldn't happen, but log and continue
k.Logger(ctx).Error("escrow account not found during withdrawal processing", "signer", signer)
continue
}
escrowAccount.Balance = escrowAccount.Balance.Sub(amount)
k.SetEscrowAccount(ctx, escrowAccount)
// Remove from both withdrawal indexes using withdrawal.AvailableTimestamp
k.DeleteWithdrawal(ctx, withdrawal)
// Emit event
event := types.NewEventWithdrawFromEscrowExecuted(signer, amount)
if err := ctx.EventManager().EmitTypedEvent(event); err != nil {
// Log error but continue - event emission failure shouldn't stop processing
k.Logger(ctx).Error("failed to emit withdrawal executed event", "error", err, "signer", signer)
}
}
}
PaymentPromise
// PaymentPromise is a promise to pay for a Fibre blob. It contains the
// commitment and payment details for the Fibre blob.
message PaymentPromise {
// chain_id is the chain ID that this payment promise is valid for.
// Example: arabica-11, mocha-4, or celestia.
string chain_id = 1;
// namespace is the namespace the blob is associated with.
bytes namespace = 2;
// blob_size is the size of the blob in bytes
uint32 blob_size = 3;
// commitment is the hash of the row root and the Random Linear Combination (RLC) root
bytes commitment = 4;
// fibre_blob_version is the version of the Fibre blob encoding
uint32 fibre_blob_version = 5;
// height is the height that is used to determine the validator set that is used
int64 height = 6;
// creation_timestamp is the timestamp when this promise was created. This
// is critical for determining which validators sign the commitment and
// determining when service stops for this blob.
google.protobuf.Timestamp creation_timestamp = 7 [(gogoproto.nullable) = false, (gogoproto.stdtime) = true];
// signer_public_key is the public key of the owner of the escrow account to charge
google.protobuf.Any signer_public_key = 8 [(cosmos_proto.accepts_interface) = "cosmos.crypto.PubKey"];
// signature is the signer (escrow account owner) secp256k1 signature over the sign bytes
bytes signature = 9;
}
Stateless Validation
chain_idmust be non-empty.namespacemust be a valid blob namespace. Must be 29 bytes.blob_sizemust be positive.commitmentmust be 32 bytes.fibre_blob_versionmust be a supported Fibre blob version.heightmust be positive.creation_timestampmust be positive.signer_public_keymust be non-empty.signaturemust be properly formatted and non-empty.
Stateful Validation
-
Verify
creation_timestampis:- less than or equal to current confirmed timestamp
- greater than (header_timestamp - withdrawal_delay)
-
Verify escrow account exists for
signer_public_key -
Verify sufficient available balance for gas cost (see Gas Consumption section). This includes all yet to be processed
PaymentPromisesthat the validator has signed over. -
Verify PaymentPromise secp256k1 signature by escrow owner over PaymentPromise sign bytes
-
Verify PaymentPromise hasn't been processed already
Sign Bytes Format
The sign bytes for a PaymentPromise secp256k1 signature are constructed by concatenating a prefix and all fields except the signature field:
sign_bytes = prefix || chain_id || signer_public_key || namespace || blob_size || commitment || fibre_blob_version || height || creation_timestamp
prefix: "fibre/pp:v0" (11 bytes)chain_id: Raw chain ID bytes (variable length)signer_public_key: Raw bytes of signer public key secp256k1 (33 bytes)namespace: Raw namespace bytes (29 bytes)blob_size: Big-endian encoded uint32 (4 bytes)commitment: Raw commitment bytes (32 bytes)fibre_blob_version: Big-endian encoded uint32 (4 bytes)height: Big-endian encoded int64 (8 bytes)creation_timestamp: UTC timestamp encoded using Go's time.Time.MarshalBinary() (variable but usually 15 bytes)
The total length of the sign bytes is: 1 + len(chain_id) + 33 + 29 + 4 + 32 + 4 + 8 + len(creation_timestamp) = 111 + len(chain_id) + len(creation_timestamp) bytes.
Payment Promise Hash
The PaymentPromise hash is calculated using the following formula:
payment_promise_hash = SHA256(sign_bytes || signature)
sign_bytes: Raw sign bytes (variable length)signature: Raw signature bytes (64 bytes)
Processed Payments Pruning
Processed payments are automatically pruned in BeginBlocker when current_time >= processed_at + payment_promise_retention_window to prevent unbounded state growth:
The pruning mechanism ensures that:
- Processed payments outside the retention window are removed to prevent unbounded state growth
- Both indexes (by hash and by time) are deleted atomically
- An event is emitted for each pruned payment for observability
- Errors in parsing or deleting individual entries don't stop the entire pruning process
MsgPayForFibre
Contains the original PaymentPromise with validator signatures, submitted by the user. Successful MsgPayForFibre transactions are included in their own reserved namespace. The commitment from the PaymentPromise is also included in the original data square in the namespace specified in the PaymentPromise.
// MsgPayForFibre contains the original PaymentPromise with validator signatures.
message MsgPayForFibre {
option (cosmos.msg.v1.signer) = "signer";
// signer is the bech32 encoded address submitting this message
string signer = 1 [(cosmos_proto.scalar) = "cosmos.AddressString"];
// payment_promise is the original PaymentPromise
PaymentPromise payment_promise = 2 [(gogoproto.nullable) = false];
// validator_signatures contains ed25519 signatures from validators
repeated bytes validator_signatures = 3;
}
Stateless Validation:
signermust be a valid addressPaymentPromisemust be valid- Must have at least one validator signature
- All validator signatures must be non-empty
Stateful Processing:
- Validate PaymentPromise
- Verify validator ed25519 signatures represent 2/3+ threshold from validator set at
promise.height(obtained via historical info query from staking module):- Signatures must represent 2/3+ of total voting power AND 2/3+ of validator count
- Each signature is verified using the validator's ed25519 public key from the validator set
- Calculate gas cost (see Gas Consumption section) and deduct from both escrow balance and available_balance
- Mark promise as processed by storing
ProcessedPaymentwithprocessed_attimestamp in both indexes:processed_payments_by_hash/{payment_promise_hash}for replay protectionprocessed_payments_by_time/{processed_at}/{payment_promise_hash}for time-ordered pruning
- Include commitment in data square
- Emit EventPayForFibre
When processing a successful MsgPayForFibre, two pieces of metadata are written to the original data square:
- The tx containing the
MsgPayForFibreis included in the reserved namespace for Fibre transactions. - A system-level blob is generated with the namespace from the PaymentPromise and the blob data is the Fibre blob commitment.
MsgPaymentPromiseTimeout
Processes a PaymentPromise after the timeout period if no MsgPayForFibre was submitted. This mechanism is critical to guaranteeing that payment occurs. MsgPaymentPromiseTimeout transactions are included in the default transaction reserved namespace. A system-level blob is not generated for this transaction.
// MsgPaymentPromiseTimeout processes a payment promise after the timeout period.
message MsgPaymentPromiseTimeout {
option (cosmos.msg.v1.signer) = "signer";
// signer is the bech32 encoded address submitting this message (can be anyone)
string signer = 1 [(cosmos_proto.scalar) = "cosmos.AddressString"];
// payment_promise is the original payment promise
PaymentPromise payment_promise = 2 [(gogoproto.nullable) = false];
}
Stateless Validation:
signermust be a valid addressPaymentPromisemust be valid
Stateful Processing:
- Validate PaymentPromise
- Verify
promise.creation_timestamp + payment_promise_timeout <= header_timestamp(timeout has passed) - Calculate gas cost (see Gas Consumption section) and deduct from both escrow balance and available_balance
- Mark promise as processed by storing
ProcessedPaymentwithprocessed_attimestamp in both indexes:processed_payments_by_hash/{payment_promise_hash}for replay protectionprocessed_payments_by_time/{processed_at}/{payment_promise_hash}for time-ordered pruning
- DO NOT include commitment in data square (since no validator consensus was reached)
- Emit EventPaymentPromiseTimeout
Automatic State Transitions
The fibre module requires automatic processing in BeginBlocker to handle time-based state transitions that cannot rely on user-submitted transactions. Two key operations must occur automatically:
- Withdrawal Processing: Transfer funds from escrow to user accounts when withdrawal delay expires (see Withdrawal Processing)
- Processed Payment Pruning: Remove old processed payments to prevent unbounded state growth (see Processed Payments Pruning)
BeginBlocker Implementation
func BeginBlocker(ctx sdk.Context, k Keeper) error {
// Process available withdrawals first (affects escrow balances)
if err := k.processAvailableWithdrawals(ctx); err != nil {
return err
}
// Prune payment promises that are outside the retention window
if err := k.pruneProcessedPayments(ctx); err != nil {
return err
}
return nil
}
Events
EventDepositToEscrow
| Attribute Key | Attribute Value |
|---|---|
| signer | {bech32 encoded signer address} |
| amount | {deposit amount} |
EventWithdrawFromEscrowRequest
| Attribute Key | Attribute Value |
|---|---|
| signer | {bech32 encoded signer address} |
| amount | {withdrawal amount} |
| requested_at | {timestamp when requested} |
| available_at | {timestamp when available} |
EventWithdrawFromEscrowExecuted
| Attribute Key | Attribute Value |
|---|---|
| signer | {bech32 encoded escrow owner} |
| amount | {withdrawal amount} |
EventPayForFibre
| Attribute Key | Attribute Value |
|---|---|
| signer | {bech32 encoded submitter address} |
| namespace | {namespace the blob is published to} |
| validator_count | {number of validator signatures} |
EventPaymentPromiseTimeout
| Attribute Key | Attribute Value |
|---|---|
| processor | {bech32 encoded processor address} |
| signer | {bech32 encoded escrow owner} |
| payment_promise_hash | {hash for the PaymentPromise that is being timed out} |
EventUpdateFibreParams
| Attribute Key | Attribute Value |
|---|---|
| signer | {bech32 encoded authority address} |
| params | {updated fibre module parameters} |
EventProcessedPaymentPruned
| Attribute Key | Attribute Value |
|---|---|
| payment_promise_hash | {hash of the PaymentPromise that was pruned} |
| processed_at | {timestamp when the payment was originally processed} |
Queries
EscrowAccount
Queries an escrow account by signer.
Request:
message QueryEscrowAccountRequest {
string signer = 1;
}
Response:
message QueryEscrowAccountResponse {
EscrowAccount escrow_account = 1;
bool found = 2;
}
Query Withdrawals
Queries withdrawals for an escrow account. Since withdrawals are automatically deleted from state when executed, this query returns all pending withdrawals for the specified signer.
Request:
message QueryWithdrawalsRequest {
string signer = 1;
cosmos.base.query.v1beta1.PageRequest pagination = 2;
}
Response:
message QueryWithdrawalsResponse {
repeated Withdrawal withdrawals = 1;
cosmos.base.query.v1beta1.PageResponse pagination = 2;
}
IsPaymentProcessed
Queries whether a payment has been processed.
Request:
message QueryIsPaymentProcessedRequest {
bytes promise_hash = 1;
}
Response:
message QueryIsPaymentProcessedResponse {
google.protobuf.Timestamp processed_at = 1;
bool found = 2;
}
ValidatePaymentPromise
Validates a PaymentPromise for server use, performing all required checks including escrow balance and processing status.
Request:
message QueryValidatePaymentPromiseRequest {
PaymentPromise promise = 1;
}
Response:
message QueryValidatePaymentPromiseResponse {
bool is_valid = 1;
}
Validation Checks:
- Verify escrow account exists and has sufficient available balance for the gas cost (see Gas Consumption section)
- Verify PaymentPromise hasn't been processed already
- Perform all standard PaymentPromise validation
Parameters
All parameters are modifiable via governance.
GasPerBlobByte
GasPerBlobByte is the amount of gas consumed per byte of blob data when a PaymentPromise is processed. This determines the gas cost for Fibre blob inclusion (default: 1).
WithdrawalDelay
WithdrawalDelay is the duration that must pass between a user requesting a withdrawal and when funds are withdrawn (default: 24 hours).
PaymentPromiseTimeout
PaymentPromiseTimeout is the duration after which anyone can submit a MsgPaymentPromiseTimeout transaction on-chain if the user hasn't submitted a MsgPayForFibre for their PaymentPromise (default: 1 hour).
PaymentPromiseRetentionWindow
PaymentPromiseRetentionWindow is the duration after which a payment promise can be pruned from the state machine (default: 24 hours).
Client
CLI
Transactions
# Deposit to escrow account
celestia-appd tx fibre deposit-to-escrow <amount> [flags]
# Request withdrawal from escrow
celestia-appd tx fibre request-withdrawal <amount> [flags]
# Submit payment with validator signatures (hex-encoded signatures)
celestia-appd tx fibre pay-for-fibre <payment_promise_json> <hex_validator_signatures> [flags]
# Submit a PaymentPromise timeout
celestia-appd tx fibre payment-promise-timeout <payment_promise_json> [flags]
CLI Queries
# Query module parameters
celestia-appd query fibre params
# Query escrow account
celestia-appd query fibre escrow-account <signer_address>
# Query withdrawals
celestia-appd query fibre withdrawals <signer_address>
# Query if PaymentPromise was processed
celestia-appd query fibre is-payment-processed <payment_promise_hash>
Indexing
Escrow Accounts:
- Primary Index:
escrow_accounts/{signer}→EscrowAccount
Withdrawals:
Withdrawals use a dual-index pattern for efficient querying:
- By signer:
withdrawals_by_signer/{signer}/{requested_timestamp}→Withdrawal(complete struct) - By availability:
withdrawals_by_available/{available_timestamp}/{signer}→Withdrawal(complete struct)
Both indexes store the full Withdrawal struct. The available_timestamp field in the struct is set at creation time and never changes, even if the WithdrawalDelay parameter changes via governance. This ensures correct deletion from both indexes.
Processed Payments:
Processed payments use a dual-index pattern for efficient replay protection and time-ordered pruning:
- By hash:
processed_payments_by_hash/{payment_promise_hash}→ProcessedPayment(complete struct, for replay protection) - By time:
processed_payments_by_time/{processed_at}/{payment_promise_hash}→ProcessedPayment(complete struct, for time-ordered pruning)
Both indexes store the full ProcessedPayment struct. This dual-index design enables:
- Fast O(1) lookup by hash to prevent double-processing of payment promises
- Efficient time-ordered iteration for automatic pruning in
BeginBlocker - Atomic deletion from both indexes when pruning occurs
Validator Address Registry
Abstract
The x/valaddr module enables validators to register their fibre service provider information.
Contents
Concepts
Fibre Service Provider
Every validator in the active set is a Fibre Service Provider (FSP). Each FSP register's their service addresses to the celestia-app state. Fibre clients encode data and send unique chunks to each FSP. In return, each FSP signs over a commitment to that data using their consensus key, indicating that they have downloaded it, verified that the encoding is uniquely decodable, and will serve that data upon request for at least the service period.
State Management
The module maintains a simple key-value store where:
- Key: Validator consensus address (celestiavalcons...)
- Value: FibreProviderInfo struct containing service details
State
The x/valaddr module stores the following data:
FibreProviderInfo
message FibreProviderInfo {
// ip_address is the IP address where users can access the fibre service
string ip_address = 1;
}
Store Keys
0x01 | ValidatorConsensusAddress -> ProtocolBuffer(FibreProviderInfo): Maps validator consensus address to fibre provider info
Messages
MsgSetFibreProviderInfo
Allows a validator to set or update their fibre provider information.
message MsgSetFibreProviderInfo {
string signer = 1;
// host is the network address for the fibre service provider (max 90 characters)
string host = 2;
}
Validation Rules:
signermust be a valid validator consensus operator addresshostmust be less than 90 characters
Events
EventSetFibreProviderInfo
Emitted when a validator sets or updates their fibre provider information.
message EventSetFibreProviderInfo {
// validator_consensus_address is the consensus address of the validator
string validator_consensus_address = 1;
// ip_address is the IP addresses for the fibre service provider
string ip_address = 2;
}
Queries
The module supports two types of queries. The first one is aimed for new fibre clients to build their address book. The second is to request the info for specific providers when a) they are added to the validator set or b) they are unreachable and thus the address may have changed.
QueryAllActiveFibreProviders
Query fibre provider information for all validators in the active set.
Request:
message QueryAllActiveFibreProvidersRequest {}
Response:
message QueryAllActiveFibreProvidersResponse {
// providers contains all active fibre providers
repeated FibreProvider providers = 1;
}
message FibreProvider {
// validator_consensus_address is the consensus address of the validator
string validator_consensus_address = 1;
// info contains the fibre provider information
FibreProviderInfo info = 2;
}
QueryFibreProviderInfo
Query fibre provider information for a specific validator.
Request:
message QueryFibreProviderInfoRequest {
// validator_consensus_address is the consensus address of the validator
string validator_consensus_address = 1;
}
Response:
message QueryFibreProviderInfoResponse {
// info contains the fibre provider information
FibreProviderInfo info = 1;
// found indicates if the validator has registered info
bool found = 2;
}
Parameters
The x/valaddr module has no parameters.
Client
CLI Commands
Query Commands:
# Query specific validator's fibre info
celestia-appd query fibre provider <validator-consensus-address>
# Query all active fibre providers
celestia-appd query fibre providers <num-providers>
Transaction Commands:
# Set fibre provider info (must be signed by validator)
celestia-appd tx fibre set-host <host-address> --from <validator-operator-key>
Encoding
What goes into the original data square?
The Fibre DA scheme does not store Fibre blob data in the original data square. Instead, the blob data is only stored in RSEMA1d rows and metadata for the Fibre blob is stored in the original data square. The two pieces of Fibre blob metadata stored in the original data square are:
-
Similar to
MsgPayForBlobs, txs that contain aMsgPayForFibreare included in their own reserved namespace. ThePAY_FOR_FIBRE_NAMESPACEis0x0000000000000000000000000000000000000000000000000000000005. Txs with this namespace are encoded as transaction shares. -
A system-level blob is generated by the state machine for each Fibre blob. It conforms to share version 2 which differs from share version 1 in that it includes the Fibre
fibre_blob_versionand the Fibre commitment:- namespace verison: 0
- namespace: the namespace specified in the
MsgPayForFibre - share version: 2
- sequence start indicator: 1
- sequence length: Fibre blob version (4 bytes) + Fibre commitment (32 bytes) = 36 bytes
- signer: the signer of the
MsgPayForFibre - fibre blob version: the version of the Fibre blob encoding
- commitment: the Fibre commitment
What goes into the RSEMA1D original rows?
Assumptions
Taken from network params:
- number of original rows = 4096
- row size = ceil(fibre blob size / number of original rows)
RSEMA1D row encoding
The Fibre blob data is encoded into RSEMA1d original rows.
If the blob content in a row does not fill the entire row, the row is padded with zeros. To differentiate between significant zeros and padding zeros, the row is prefixed with a length.
Note: this diagram uses a row length of 64 bytes but the actual row length can be a multiple of 64 bytes.